Bayesian statistics in health economic evaluations - part 2

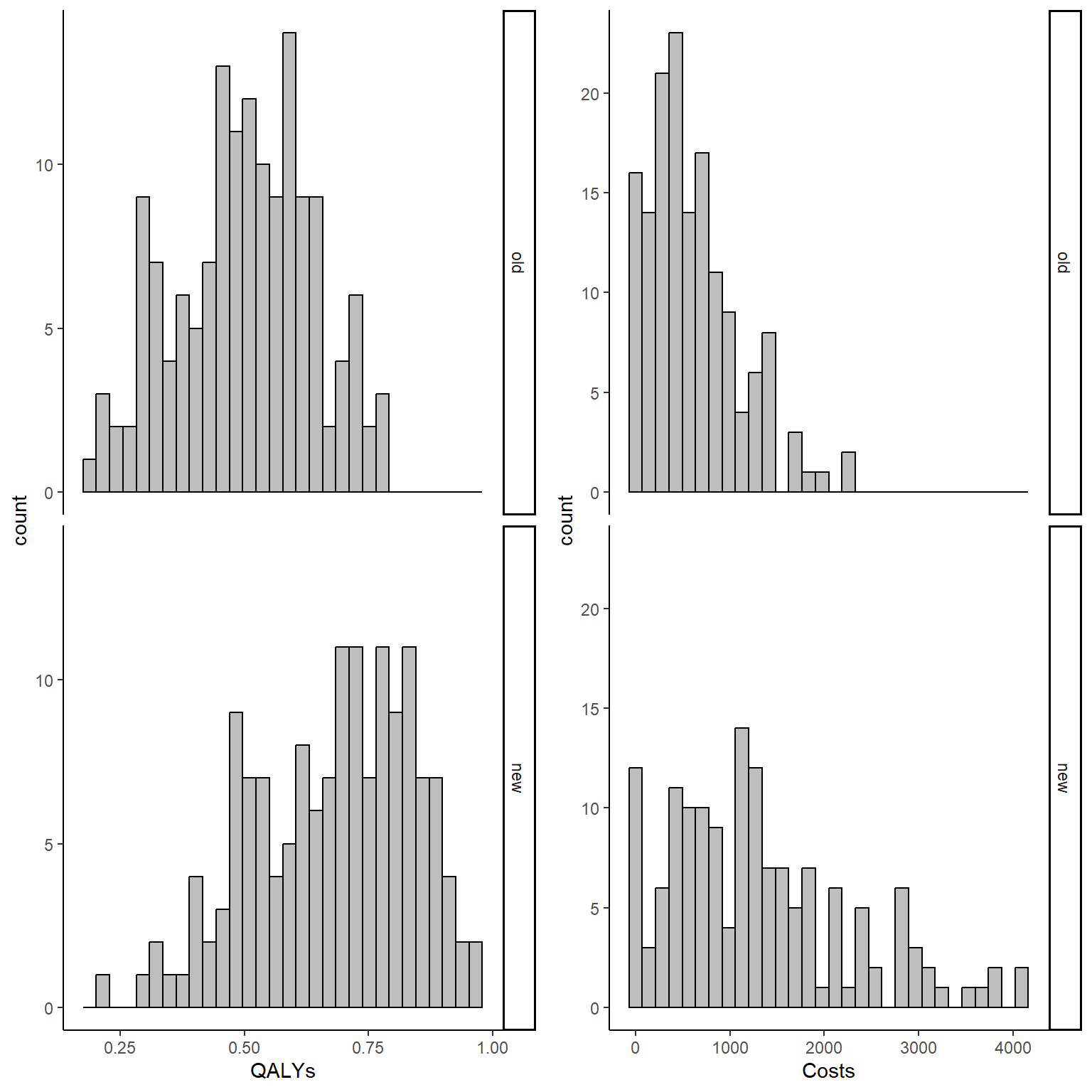
Step 1: fit a standard normal model

As in the previous post, we rely on factoring the joint distribution \(p(e,c\mid \boldsymbol \theta)\) into the product of a marginal distribution \(p(e\mid \boldsymbol \theta_e)\) of the effects and a conditional distribution \(p(c \mid e, \boldsymbol \theta_c)\) of the cost given the effects, each indexed by corresponding set of parameters. We can rely on the freely-available Bayesian software named JAGS to fit the model. We write the model code into a txt file and save it into our current wd to be called from R. Then, we load the package R2jags which allows to call the software from R through the function jags and after providing the data and some technical parameters needed to run the model.

#save data input
n <- dim(data_sim_ec)[1]
QALYs <- data_sim_ec$QALYs
Costs <- data_sim_ec$Costs
trt <- data_sim_ec$trt

#load package and provide algorithm parameters
library(R2jags)
set.seed(2345) #set seed for reproducibility
datalist<-list("n","QALYs","Costs","trt") #pass data into a list
#set up initial values for algorithm
inits1 <- list(.RNG.name = "base::Wichmann-Hill", .RNG.seed = 1)
inits2 <- list(.RNG.name = "base::Wichmann-Hill", .RNG.seed = 2)
#set parameter easimates to save
params<-c("beta0","beta1","gamma0","gamma1","gamma2","s_c","s_e","nu_c","nu_e")
filein<-"model_bn.txt" #name of model file
n.iter<-20000 #n of iterations

#fit model
jmodel_bn<-jags(data=datalist,inits=list(inits1,inits2),
                parameters.to.save=params,model.file=filein,
                n.chains=2,n.iter=n.iter,n.thin=1)

# Compiling model graph
#    Resolving undeclared variables
#    Allocating nodes
# Graph information:
#    Observed stochastic nodes: 600
#    Unobserved stochastic nodes: 7
#    Total graph size: 1522
# 
# Initializing model

We then proceed to extract the key quantities of interest of this analysis by post-processing the model estimates via simulation methods, with the aim to obtain the mean effects and costs outcome posterior distributions \((\mu_e,\mu_c)\) in each treatment group.

#obtain estimates of means by arm

#extract estimates for each mean parameter by trt group
nu_e0 <- jmodel_bn$BUGSoutput$sims.list$nu_e[,trt==0]
nu_e1 <- jmodel_bn$BUGSoutput$sims.list$nu_e[,trt==1]
nu_c0 <- jmodel_bn$BUGSoutput$sims.list$nu_c[,trt==0]
nu_c1 <- jmodel_bn$BUGSoutput$sims.list$nu_c[,trt==1]
#extract estimates for std
s_e <- jmodel_bn$BUGSoutput$sims.list$s_e
s_c <- jmodel_bn$BUGSoutput$sims.list$s_c

#create empty vectors to contain results for means by trt group
mu_e0 <- mu_c0 <- c()
mu_e1 <- mu_c1 <- c()

#set number of replications
L <- 5000

set.seed(2345) #set seed for reproducibility
#generate replications and take mean at each iteration of the posterior
for(i in 1:n.iter){
 mu_e0[i] <- mean(rnorm(L,nu_e0[i,],s_e[i])) 
 mu_e1[i] <- mean(rnorm(L,nu_e1[i,],s_e[i]))
 mu_c0[i] <- mean(rnorm(L,nu_c0[i,],s_c[i])) 
 mu_c1[i] <- mean(rnorm(L,nu_c1[i,],s_c[i])) 
}

#calculate mean differences
Delta_e <- mu_e1 - mu_e0
Delta_c <- mu_c1 - mu_c0

Step 2: fit a Beta-Gamma model

As a comparative approach, we now try to directly address the skewness in the observed data by using a Beta distribution for modelling the QALYs and a Gamma distribution for the Total costs. The main idea is that, by using distributions that can naturally allow for non-symmetric data, estimates will likely be more robust and uncertainty concerning such estimates will be more properly quantified. We begin by writing the model file and save it as a txt file.

model_bg <- "
model {

#model specification
for(i in 1:n){
      QALYs[i]~dbeta(shape1[i],shape2[i])
      shape1[i]<-nu_e[i]*(nu_e[i]*(1-nu_e[i])/pow(s_e,2) - 1)
      shape2[i]<-(1-nu_e[i])*(nu_e[i]*(1-nu_e[i])/pow(s_e,2) - 1)
      logit(nu_e[i])<-beta0 + beta1*trt[i]

      Costs[i]~dgamma(shape[i],rate[i])
      shape[i]<-pow(nu_c[i],2)/pow(s_c,2)
      rate[i]<-nu_c[i]/pow(s_c,2)
      log(nu_c[i])<-gamma0 + gamma1*trt[i] + gamma2*QALYs[i]
}

#prior specification
s_c ~ dunif(0,1000)
s_e_limit<- sqrt(0.5885263*(1-0.5885263))
s_e ~ dunif(0,s_e_limit)
beta0 ~ dnorm(0,0.001)
beta1 ~ dnorm(0,0.001)
gamma0 ~ dnorm(0,0.001)
gamma1 ~ dnorm(0,0.001)
gamma2 ~ dnorm(0,0.001)

}
"
writeLines(model_bg, con = "model_bg.txt")

We then proceed to pass the data and algorithm parameters to fit the model in JAGS. It is important to stress that, since Gamma and Beta are defined within bounds of \((0,+\infty)\) and \((0,1)\), then we need to “modify” the data to ensure that such extremes are not present (in case they occur). This is often done by adding/subtracting a small constant to the data.

#save data input
n <- dim(data_sim_ec)[1]
QALYs <- data_sim_ec$QALYs - 0.001
Costs <- data_sim_ec$Costs + 0.001
trt <- data_sim_ec$trt

#load package and provide algorithm parameters
library(R2jags)
set.seed(2345) #set seed for reproducibility
datalist<-list("n","QALYs","Costs","trt") #pass data into a list
#set up initial values for algorithm
inits1 <- list(.RNG.name = "base::Wichmann-Hill", .RNG.seed = 1)
inits2 <- list(.RNG.name = "base::Wichmann-Hill", .RNG.seed = 2)
#set parameter easimates to save
params<-c("beta0","beta1","gamma0","gamma1","gamma2","s_c","s_e","nu_c","nu_e",
          "shape","rate","shape1","shape2")
filein<-"model_bg.txt" #name of model file
n.iter<-20000 #n of iterations

#fit model
jmodel_bg<-jags(data=datalist,inits=list(inits1,inits2),
                parameters.to.save=params,model.file=filein,
                n.chains=2,n.iter=n.iter,n.thin=1)

# Compiling model graph
#    Resolving undeclared variables
#    Allocating nodes
# Graph information:
#    Observed stochastic nodes: 600
#    Unobserved stochastic nodes: 7
#    Total graph size: 2739
# 
# Initializing model

We then proceed to extract the key quantities of interest of this analysis by post-processing the model estimates via simulation methods, with the aim to obtain the mean effects and costs outcome posterior distributions \((\mu_e,\mu_c)\) in each treatment group.

#obtain estimates of means by arm

#extract estimates for each mean parameter by trt group
shape1_e0 <- jmodel_bg$BUGSoutput$sims.list$shape1[,trt==0]
shape1_e1 <- jmodel_bg$BUGSoutput$sims.list$shape1[,trt==1]
shape2_e0 <- jmodel_bg$BUGSoutput$sims.list$shape2[,trt==0]
shape2_e1 <- jmodel_bg$BUGSoutput$sims.list$shape2[,trt==1]

shape_c0 <- jmodel_bg$BUGSoutput$sims.list$shape[,trt==0]
shape_c1 <- jmodel_bg$BUGSoutput$sims.list$shape[,trt==1]
rate_c0 <- jmodel_bg$BUGSoutput$sims.list$rate[,trt==0]
rate_c1 <- jmodel_bg$BUGSoutput$sims.list$rate[,trt==1]
scale_c0 <- 1/rate_c0
scale_c1 <- 1/rate_c1


#create empty vectors to contain results for means by trt group
mu_e0_bg <- mu_c0_bg <- c()
mu_e1_bg <- mu_c1_bg <- c()

#set number of replications
L <- 5000

set.seed(2345) #set seed for reproducibility
#generate replications and take mean at each iteration of the posterior
for(i in 1:n.iter){
 mu_e0_bg[i] <- mean(rbeta(L,shape1 =  shape1_e0[i,], shape2 =  shape2_e0[i])) 
 mu_e1_bg[i] <- mean(rbeta(L,shape1 =  shape1_e1[i,], shape2 =  shape2_e1[i]))
 mu_c0_bg[i] <- mean(rgamma(L,shape =  shape_c0[i,],scale =  scale_c0[i])) 
 mu_c1_bg[i] <- mean(rgamma(L,shape =  shape_c1[i,],scale =  scale_c1[i])) 
}

#calculate mean differences
Delta_e_bg <- mu_e1_bg - mu_e0_bg
Delta_c_bg <- mu_c1_bg - mu_c0_bg

At this point it would be wise to check the results of both models and compare them in terms of some measures of relative or absolute performance, such as information criteria or posterior predictive checks. In general, the idea is that IC should reveal a better performance of the distributions that better fit the observed data, while PPCs can be used to detect possible problems in the model replications that may fail to capture some aspects of the observed data. These can be used to decide which model should be trusted more in terms of relative fit to the data. For the sake of simplicity, here I omit these comparisons as it is something I would like to dedicate a more substantial discussion.

Finally, we can then produce all standard CEA output, e.g. CEAC or CE Plane, by post-processing these posterior distributions and compare the cost-effectivenss results of the two models fitted. If you want to skip the fun, we can take advantage of the R package BCEA which is dedicated to post-processing the results from a Bayesian CEA model.

#load package and provide means e and c by group as input 
library(BCEA)
mu_e_bn <- cbind(mu_e0,mu_e1)
mu_c_bn <- cbind(mu_c0,mu_c1)
mu_e_bg <- cbind(mu_e0_bg,mu_e1_bg)
mu_c_bg <- cbind(mu_c0_bg,mu_c1_bg)

#produce CEA output
cea_res_bn <- bcea(eff = mu_e_bn, cost = mu_c_bn, ref = 2)
cea_res_bg <- bcea(eff = mu_e_bg, cost = mu_c_bg, ref = 2)

#CE Plane (set wtp value)
cep_bn <- ceplane.plot(cea_res_bn, graph = "ggplot2", wtp = 10000)
cep_bg <- ceplane.plot(cea_res_bg, graph = "ggplot2", wtp = 10000)

#CEAC 
ceac_bn <- ceac.plot(cea_res_bn, graph = "ggplot2")
ceac_bg <- ceac.plot(cea_res_bg, graph = "ggplot2")

gridExtra::grid.arrange(cep_bn, cep_bg, ceac_bn, ceac_bg, nrow = 2, ncol = 2)

# Warning: Using linewidth for a discrete variable is not advised.
# Using linewidth for a discrete variable is not advised.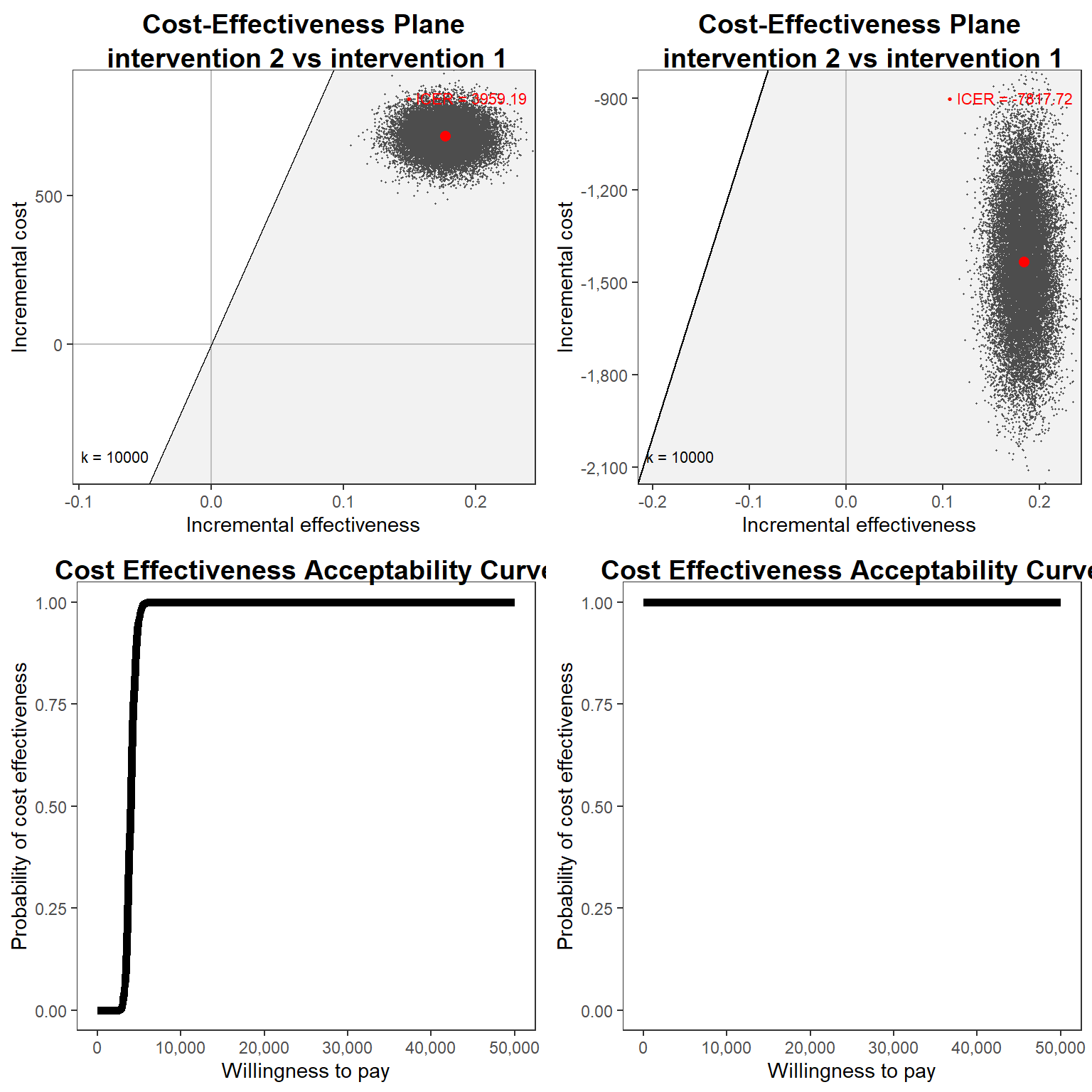

#other output
summary(cea_res_bn)

# 
# Cost-effectiveness analysis summary 
# 
# Reference intervention:  intervention 2
# Comparator intervention: intervention 1
# 
# Optimal decision: choose intervention 1 for k < 4000 and intervention 2 for k >= 4000
# 
# 
# Analysis for willingness to pay parameter k = 25000
# 
#                Expected net benefit
# intervention 1                11911
# intervention 2                15635
# 
#                                     EIB CEAC   ICER
# intervention 2 vs intervention 1 3724.1    1 3959.2
# 
# Optimal intervention (max expected net benefit) for k = 25000: intervention 2
#                 
# EVPI -1.5852e-13

summary(cea_res_bg)

# 
# Cost-effectiveness analysis summary 
# 
# Reference intervention:  intervention 2
# Comparator intervention: intervention 1
# 
# intervention 2 dominates for all k in [0 - 50000] 
# 
# 
# Analysis for willingness to pay parameter k = 25000
# 
#                Expected net benefit
# intervention 1               8507.6
# intervention 2              14523.2
# 
#                                     EIB CEAC    ICER
# intervention 2 vs intervention 1 6015.6    1 -7817.7
# 
# Optimal intervention (max expected net benefit) for k = 25000: intervention 2
#                 
# EVPI -6.3236e-13

In the end results may be quite different between the models used and it is crucial that model selection is done based on appropriate criteria in order to decide which results to trust more according to how well the model fit the data and potential issues in MCMC convergence (i.e. need to check algorithm diagnostics to make sure posterior estimates are reliable). I really think that, especially in a HTA context, Bayesian methods are naturally suited for the job since they allow to flexibly define your model to tackle different aspects of the data while also addressing uncertainty in a structural and consistent way, being it uncertainty about model estimates, missing values, predictions, etc…. Although the same can also be achieved within a frequentist framework, this comes at the cost of an increasingly complex implementation effort (e.g. need to combine bootstrapping and non-normal distributions) which, instead, in a Bayesian setting can be achieved in a relatively easy way. As the models we need to fit become increasingly complex, it makes sense to me that more flexible approaches that can be tailored to deal with different situations and peculiarities should become more and useful to analysts to accomplish their tasks.