Introduction

In trial-based economic evaluation, some individuals are typically associated with missing data at some time point, so that their corresponding aggregated outcomes (eg, quality-adjusted life-years) cannot be evaluated. Restricting the analysis to the complete cases is inefficient and can result in biased estimates, while imputation methods are often implemented under a missing at random (MAR) assumption. We propose the use of joint longitudinal models to extend standard approaches by taking into account the longitudinal structure to improve the estimation of the targeted quantities under MAR.

Standard approach in trial-based CEA

According to recent reviews, standard practice in trial-based CEAs handles missingness at the level of the aggregated outcomes and baseline variables. Indeed, estimates of interest are obtained by directly modeling the aggregated outcomes rather than the utility and cost data at each time. This requires the analyst to process the data collected on individual $i$ at time $j$ in treatment $t$, to derive the aggregated measures over the study duration.

The following Figure shows a typical data set of trial-based CEA, formed by the sets of utility and cost variables collected at baseline $j = 0$ and some follow-ups $j = 1,…,J$. The graph represents the standard procedure for processing the data and identifying the variables used in the analysis.

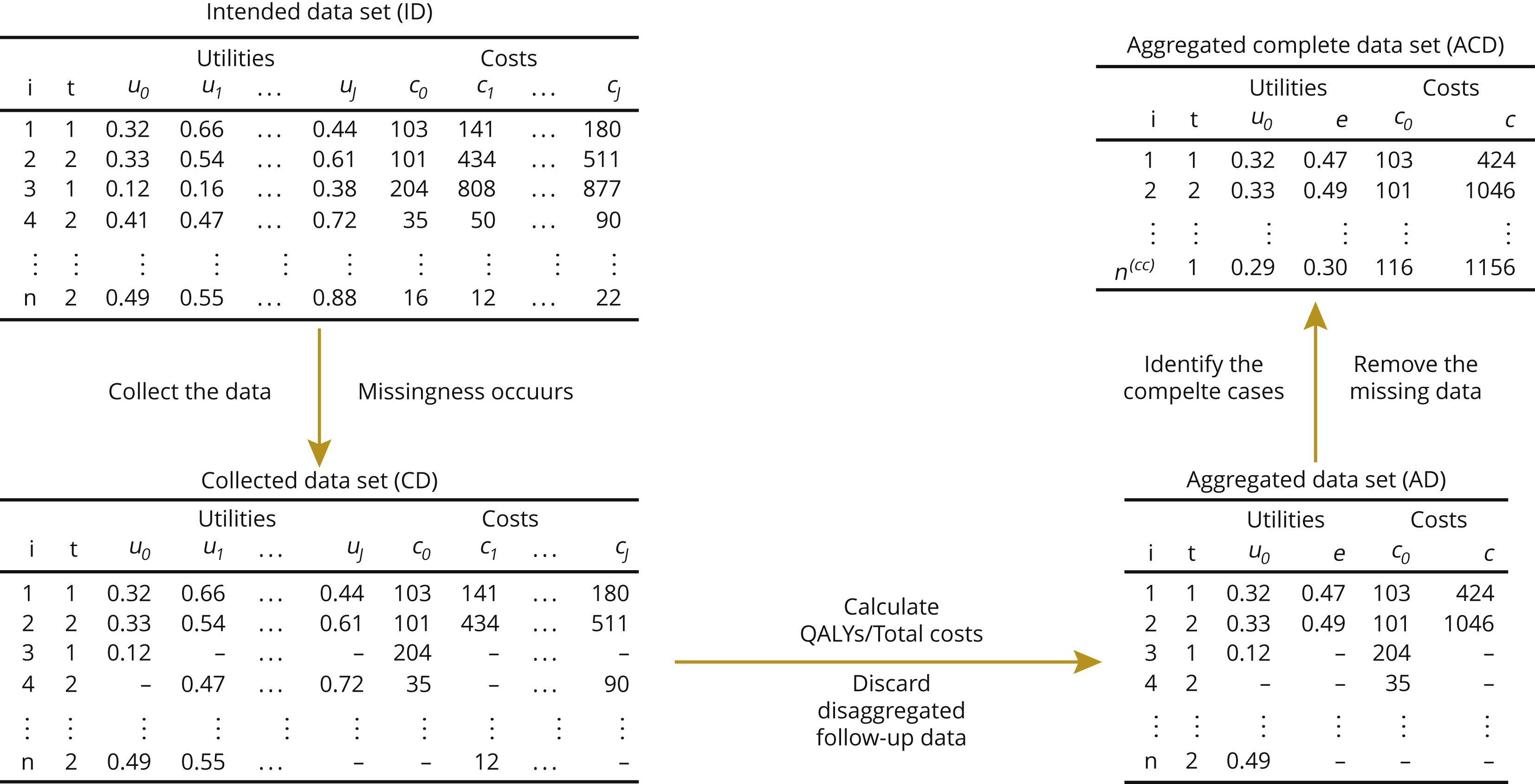
A general limitation of any aggregated method is to ignore the longitudinal nature of the data and discard all follow-up values for partially observed individuals. Conversely, methods that handle missingness at each time point account for the longitudinal structure, incorporate all available evidence, and potentially make the missingness assumptions (e.g., missing at random or MAR) more reasonable.

Methods

We propose the use of joint longitudinal models to extend standard approaches by taking into account the longitudinal structure to improve the estimation of the targeted quantities under MAR.

We compare the results from methods that handle missingness at an aggregated (case deletion, baseline imputation, and joint aggregated models) and disaggregated (joint longitudinal models) level under MAR. The methods are compared using a simulation study and applied to data from 2 real case studies.

Conclusions

Joint longitudinal models provide an alternative and potentially less biased approach for handling missing data with respect to current practice under a missing at random assumption.

Methods that ignore some of the available information may be associated with biased results and mislead the decision-making process.

This is a potentially serious issue for those who use these evaluations in their decision making, thus possibly leading to incorrect policy decisions about the cost-effectiveness of new treatment options.