Randomised Complete Block Anova (JAGS)
This tutorial will focus on the use of Bayesian estimation to fit simple linear regression models. BUGS (Bayesian inference Using Gibbs Sampling) is an algorithm and supporting language (resembling R) dedicated to performing the Gibbs sampling implementation of Markov Chain Monte Carlo (MCMC) method. Dialects of the BUGS language are implemented within three main projects:
OpenBUGS - written in component pascal.
JAGS - (Just Another Gibbs Sampler) - written in
C++.STAN - a dedicated Bayesian modelling framework written in
C++and implementing Hamiltonian MCMC samplers.
Whilst the above programs can be used stand-alone, they do offer the rich data pre-processing and graphical capabilities of R, and thus, they are best accessed from within R itself. As such there are multiple packages devoted to interfacing with the various software implementations:
R2OpenBUGS - interfaces with
OpenBUGSR2jags - interfaces with
JAGSrstan - interfaces with
STAN
This tutorial will demonstrate how to fit models in JAGS (Plummer (2004)) using the package R2jags (Su et al. (2015)) as interface, which also requires to load some other packages.
Overview
Introduction
In the previous tutorial (nested ANOVA), we introduced the concept of employing sub-replicates that are nested within the main treatment levels as a means of absorbing some of the unexplained variability that would otherwise arise from designs in which sampling units are selected from amongst highly heterogeneous conditions. Such (nested) designs are useful in circumstances where the levels of the main treatment (such as burnt and un-burnt sites) occur at a much larger temporal or spatial scale than the experimental/sampling units (e.g. vegetation monitoring quadrats). For circumstances in which the main treatments can be applied (or naturally occur) at the same scale as the sampling units (such as whether a stream rock is enclosed by a fish proof fence or not), an alternative design is available. In this design (randomised complete block design), each of the levels of the main treatment factor are grouped (blocked) together (in space and/or time) and therefore, whilst the conditions between the groups (referred to as “blocks”) might vary substantially, the conditions under which each of the levels of the treatment are tested within any given block are far more homogeneous.
If any differences between blocks (due to the heterogeneity) can account for some of the total variability between the sampling units (thereby reducing the amount of variability that the main treatment(s) failed to explain), then the main test of treatment effects will be more powerful/sensitive. As an simple example of a randomised complete block (RCB) design, consider an investigation into the roles of different organism scales (microbial, macro invertebrate and vertebrate) on the breakdown of leaf debris packs within streams. An experiment could consist of four treatment levels - leaf packs protected by fish-proof mesh, leaf packs protected by fine macro invertebrate exclusion mesh, leaf packs protected by dissolving antibacterial tablets, and leaf packs relatively unprotected as controls. As an acknowledgement that there are many other unmeasured factors that could influence leaf pack breakdown (such as flow velocity, light levels, etc) and that these are likely to vary substantially throughout a stream, the treatments are to be arranged into groups or “blocks” (each containing a single control, microbial, macro invertebrate and fish protected leaf pack). Blocks of treatment sets are then secured in locations haphazardly selected throughout a particular reach of stream. Importantly, the arrangement of treatments in each block must be randomized to prevent the introduction of some systematic bias - such as light angle, current direction etc.
Blocking does however come at a cost. The blocks absorb both unexplained variability as well as degrees of freedom from the residuals. Consequently, if the amount of the total unexplained variation that is absorbed by the blocks is not sufficiently large enough to offset the reduction in degrees of freedom (which may result from either less than expected heterogeneity, or due to the scale at which the blocks are established being inappropriate to explain much of the variation), for a given number of sampling units (leaf packs), the tests of main treatment effects will suffer power reductions. Treatments can also be applied sequentially or repeatedly at the scale of the entire block, such that at any single time, only a single treatment level is being applied (see the lower two sub-figures above). Such designs are called repeated measures. A repeated measures ANOVA is to an single factor ANOVA as a paired t-test is to a independent samples t-test. One example of a repeated measures analysis might be an investigation into the effects of a five different diet drugs (four doses and a placebo) on the food intake of lab rats. Each of the rats (“subjects”) is subject to each of the four drugs (within subject effects) which are administered in a random order. In another example, temporal recovery responses of sharks to bi-catch entanglement stresses might be simulated by analyzing blood samples collected from captive sharks (subjects) every half hour for three hours following a stress inducing restraint. This repeated measures design allows the anticipated variability in stress tolerances between individual sharks to be accounted for in the analysis (so as to permit more powerful test of the main treatments). Furthermore, by performing repeated measures on the same subjects, repeated measures designs reduce the number of subjects required for the investigation. Essentially, this is a randomised complete block design except that the within subject (block) effect (e.g. time since stress exposure) cannot be randomised.
To suppress contamination effects resulting from the proximity of treatment sampling units within a block, units should be adequately spaced in time and space. For example, the leaf packs should not be so close to one another that the control packs are effected by the antibacterial tablets and there should be sufficient recovery time between subsequent drug administrations. In addition, the order or arrangement of treatments within the blocks must be randomized so as to prevent both confounding as well as computational complications. Whilst this is relatively straight forward for the classic randomized complete block design (such as the leaf packs in streams), it is logically not possible for repeated measures designs. Blocking factors are typically random factors that represent all the possible blocks that could be selected. As such, no individual block can truly be replicated. Randomised complete block and repeated measures designs can therefore also be thought of as un-replicated factorial designs in which there are two or more factors but that the interactions between the blocks and all the within block factors are not replicated.
Linear models
The linear models for two and three factor nested design are:
\[ y_{ij} = \mu + \beta_i + \alpha_j + \epsilon_{ij},\]
\[ y_{ijk} = \mu + \beta_i + \alpha_j + \gamma_k + (\beta\alpha)_{ij} + (\beta\gamma)_{ik} + (\alpha\gamma)_{jk} + (\alpha\beta\gamma)_{ijk} + \epsilon_{ijk}, \;\;\; \text{(Model 1)}\]
\[ y_{ijk} = \mu + \beta_i + \alpha_j + \gamma_k + (\alpha\gamma)_{jk} + \epsilon_{ijk}, \;\;\; \text{(Model 2)},\]
where \(\mu\) is the overall mean, \(\beta\) is the effect of the Blocking Factor B (\(\sum \beta=0\)), \(\alpha\) and \(\gamma\) are the effects of withing block Factor A and Factor C, respectively, and \(\epsilon \sim N(0,\sigma^2)\) is the random unexplained or residual component.
Tests for the effects of blocks as well as effects within blocks assume that there are no interactions between blocks and the within block effects. That is, it is assumed that any effects are of similar nature within each of the blocks. Whilst this assumption may well hold for experiments that are able to consciously set the scale over which the blocking units are arranged, when designs utilize arbitrary or naturally occurring blocking units, the magnitude and even polarity of the main effects are likely to vary substantially between the blocks. The preferred (non-additive or “Model 1”) approach to un-replicated factorial analysis of some bio-statisticians is to include the block by within subject effect interactions (e.g. \(\beta\alpha\)). Whilst these interaction effects cannot be formally tested, they can be used as the denominators in F-ratio calculations of their respective main effects tests. Proponents argue that since these blocking interactions cannot be formally tested, there is no sound inferential basis for using these error terms separately. Alternatively, models can be fitted additively (“Model 2”) whereby all the block by within subject effect interactions are pooled into a single residual term (\(\epsilon\)). Although the latter approach is simpler, each of the within subject effects tests do assume that there are no interactions involving the blocks and that perhaps even more restrictively, that sphericity holds across the entire design.
Assumptions
As with other ANOVA designs, the reliability of hypothesis tests is dependent on the residuals being:
normally distributed. Boxplots using the appropriate scale of replication (reflecting the appropriate residuals/F-ratio denominator should be used to explore normality. Scale transformations are often useful.
equally varied. Boxplots and plots of means against variance (using the appropriate scale of replication) should be used to explore the spread of values. Residual plots should reveal no patterns. Scale transformations are often useful.
independent of one another. Although the observations within a block may not strictly be independent, provided the treatments are applied or ordered randomly within each block or subject, within block proximity effects on the residuals should be random across all blocks and thus the residuals should still be independent of one another. Nevertheless, it is important that experimental units within blocks are adequately spaced in space and time so as to suppress contamination or carryover effects.
Simple RCB
Data generation
Imagine we has designed an experiment in which we intend to measure a response (y) to one of treatments (three levels; “a1,” “a2” and “a3”). Unfortunately, the system that we intend to sample is spatially heterogeneous and thus will add a great deal of noise to the data that will make it difficult to detect a signal (impact of treatment). Thus in an attempt to constrain this variability you decide to apply a design (RCB) in which each of the treatments within each of 35 blocks dispersed randomly throughout the landscape. As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped.
> library(plyr)
> set.seed(123)
> nTreat <- 3
> nBlock <- 35
> sigma <- 5
> sigma.block <- 12
> n <- nBlock*nTreat
> Block <- gl(nBlock, k=1)
> A <- gl(nTreat,k=1)
> dt <- expand.grid(A=A,Block=Block)
> #Xmat <- model.matrix(~Block + A + Block:A, data=dt)
> Xmat <- model.matrix(~-1+Block + A, data=dt)
> block.effects <- rnorm(n = nBlock, mean = 40, sd = sigma.block)
> A.effects <- c(30,40)
> all.effects <- c(block.effects,A.effects)
> lin.pred <- Xmat %*% all.effects
>
> # OR
> Xmat <- cbind(model.matrix(~-1+Block,data=dt),model.matrix(~-1+A,data=dt))
> ## Sum to zero block effects
> block.effects <- rnorm(n = nBlock, mean = 0, sd = sigma.block)
> A.effects <- c(40,70,80)
> all.effects <- c(block.effects,A.effects)
> lin.pred <- Xmat %*% all.effects
>
>
>
> ## the quadrat observations (within sites) are drawn from
> ## normal distributions with means according to the site means
> ## and standard deviations of 5
> y <- rnorm(n,lin.pred,sigma)
> data.rcb <- data.frame(y=y, expand.grid(A=A, Block=Block))
> head(data.rcb) #print out the first six rows of the data set
y A Block
1 45.80853 1 1
2 66.71784 2 1
3 93.29238 3 1
4 43.10101 1 2
5 73.20697 2 2
6 91.77487 3 2Exploratory data analysis
Normality and Homogeneity of variance
> boxplot(y~A, data.rcb)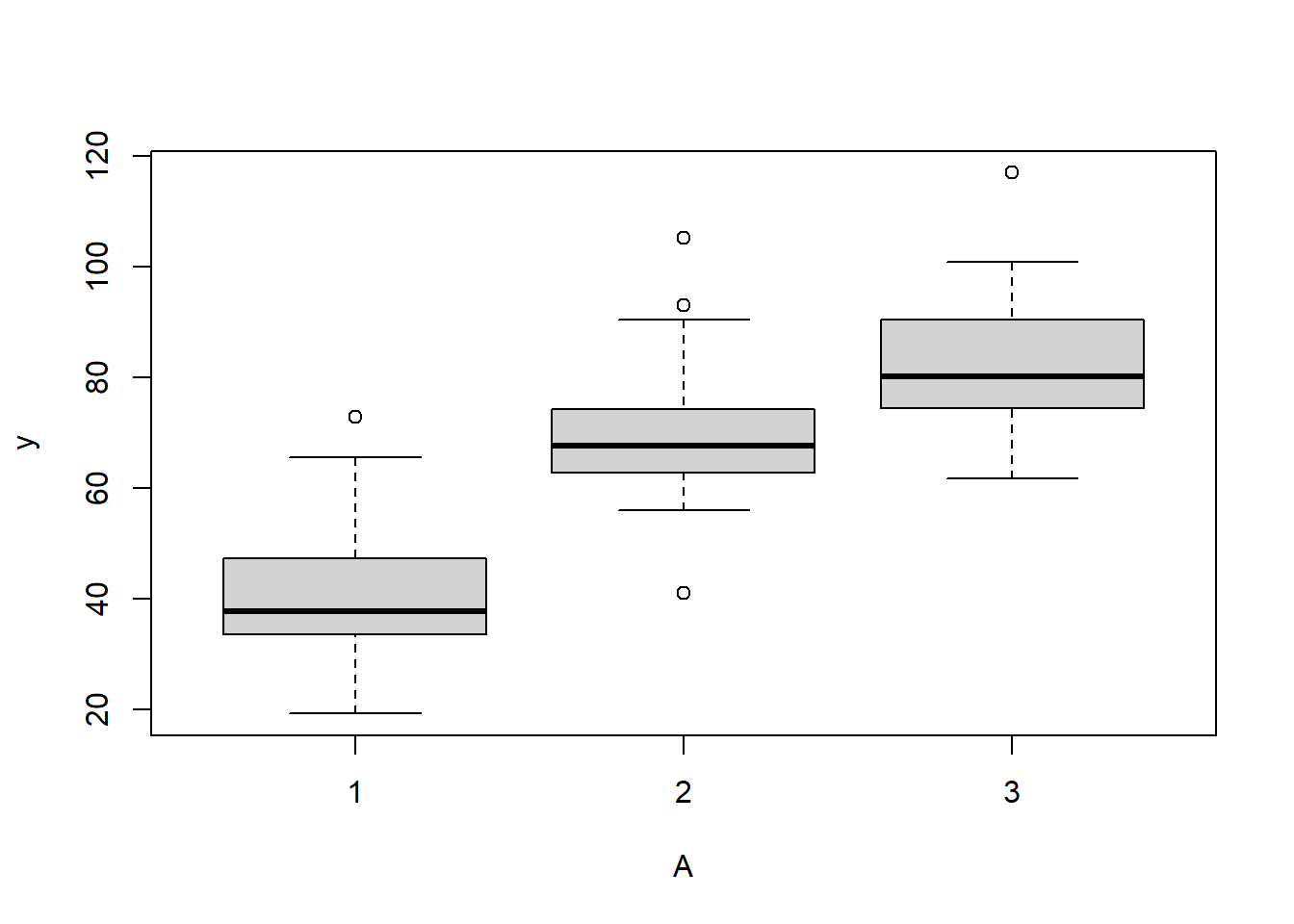
Conclusions:
there is no evidence that the response variable is consistently non-normal across all populations - each boxplot is approximately symmetrical.
there is no evidence that variance (as estimated by the height of the boxplots) differs between the five populations. . More importantly, there is no evidence of a relationship between mean and variance - the height of boxplots does not increase with increasing position along the \(y\)-axis. Hence it there is no evidence of non-homogeneity
Obvious violations could be addressed either by:
- transform the scale of the response variables (to address normality, etc). Note transformations should be applied to the entire response variable (not just those populations that are skewed).
Block by within-Block interaction
> library(car)
> with(data.rcb, interaction.plot(A,Block,y))
>
> #OR with ggplot
> library(ggplot2)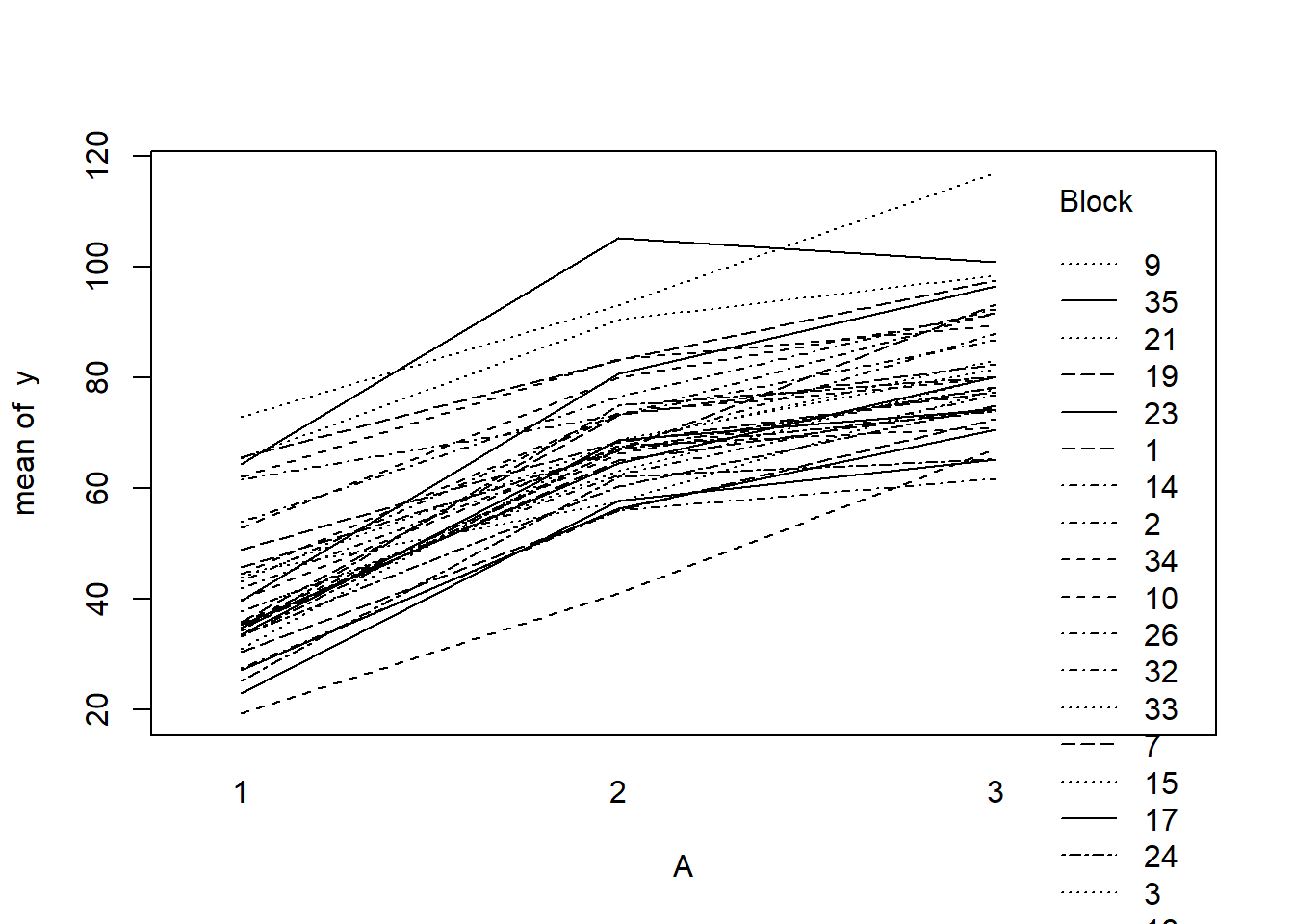
> ggplot(data.rcb, aes(y=y, x=A, group=Block,color=Block)) + geom_line() +
+ guides(color=guide_legend(ncol=3))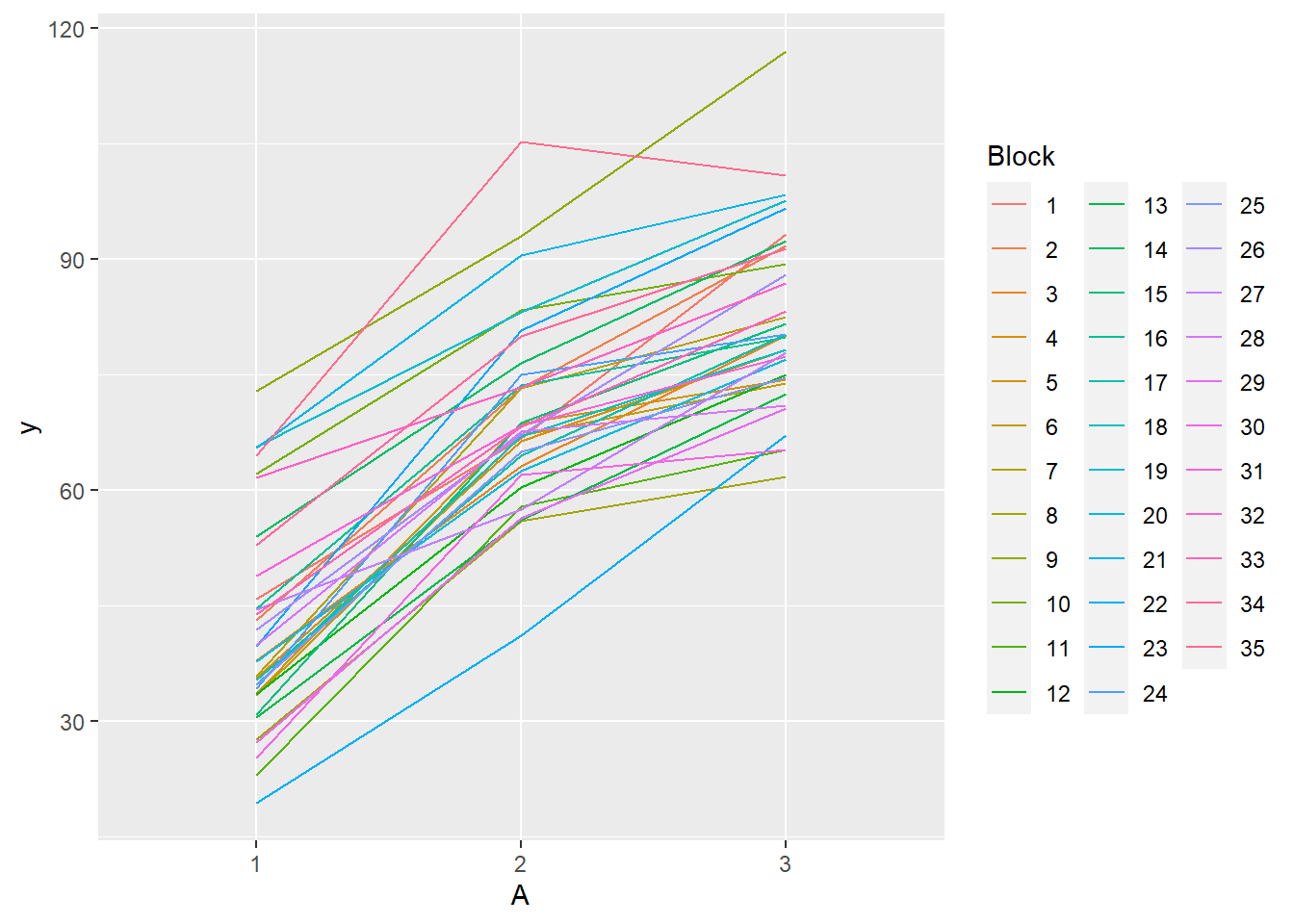
>
> residualPlots(lm(y~Block+A, data.rcb))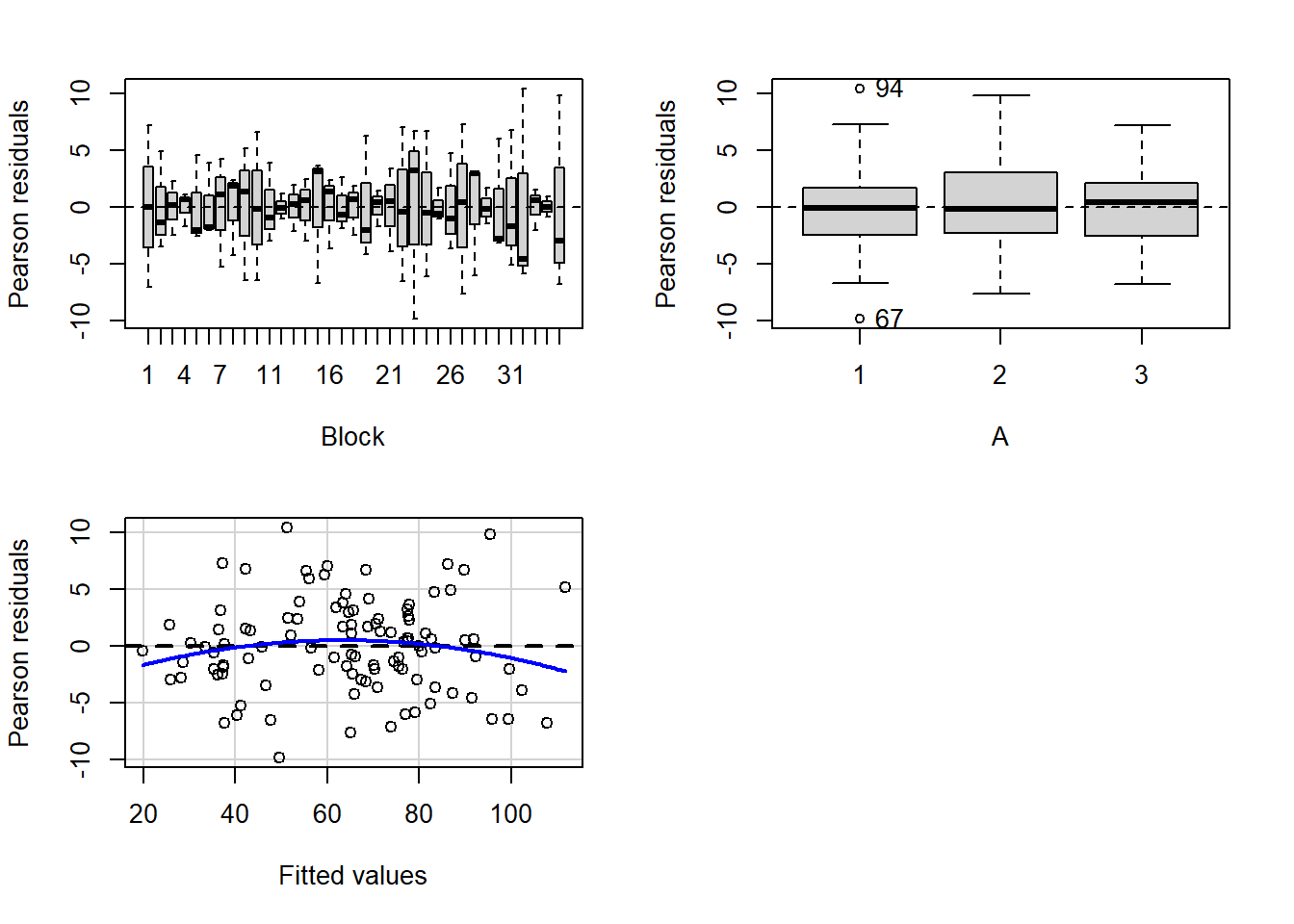
Test stat Pr(>|Test stat|)
Block
A
Tukey test -1.4163 0.1567
>
> # the Tukey's non-additivity test by itself can be obtained via an internal function
> # within the car package
> car:::tukeyNonaddTest(lm(y~Block+A, data.rcb))
Test Pvalue
-1.4163343 0.1566776
>
> # alternatively, there is also a Tukey's non-additivity test within the
> # asbio package
> library(asbio)
> with(data.rcb,tukey.add.test(y,A,Block))
Tukey's one df test for additivity
F = 2.0060029 Denom df = 67 p-value = 0.1613102Conclusions:
- there is no visual or inferential evidence of any major interactions between Block and the within-Block effect (A). Any trends appear to be reasonably consistent between Blocks.
Model fitting
Full parameterisation
\[ y_{ijk} \sim N(\mu_{ij}, \sigma^2), \;\;\; \mu_{ij}=\beta_0 + \beta_i + \gamma_{j(i)}, \]
where \(\gamma_{ij)} \sim N(0, \sigma^2_B)\), \(\beta_0, \beta_i \sim N(0, 1000000)\), and \(\sigma^2, \sigma^2_B \sim \text{Cauchy(0, 25)}\). The full parameterisation, shows the effects parameterisation in which there is an intercept (\(\beta_0\)) and two treatment effects (\(\beta_i\), where \(i\) is \(1,2\)).
Matrix parameterisation
\[ y_{ijk} \sim N(\mu_{ij}, \sigma^2), \;\;\; \mu_{ij}=\boldsymbol \beta \boldsymbol X + \gamma_{j(i)}, \]
where \(\gamma_{ij} \sim N(0, \sigma^2_B)\), \(\boldsymbol \beta \sim MVN(0, 1000000)\), and \(\sigma^2, \sigma^2_B \sim \text{Cauchy(0, 25)}\). The full parameterisation, shows the effects parameterisation in which there is an intercept (\(\alpha_0\)) and two treatment effects (\(\beta_i\), where \(i\) is \(1,2\)). The matrix parameterisation is a compressed notation, In this parameterisation, there are three alpha parameters (one representing the mean of treatment a1, and the other two representing the treatment effects (differences between a2 and a1 and a3 and a1). In generating priors for each of these three alpha parameters, we could loop through each and define a non-informative normal prior to each (as in the Full parameterisation version). However, it turns out that it is more efficient (in terms of mixing and thus the number of necessary iterations) to define the priors from a multivariate normal distribution. This has as many means as there are parameters to estimate (\(3\)) and a \(3\times3\) matrix of zeros and \(100\) in the diagonals.
\[ \boldsymbol \mu = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}, \;\;\; \sigma^2 \sim \begin{bmatrix} 1000000 & 0 & 0 \\ 0 & 1000000 & 0 \\ 0 & 0 & 1000000 \end{bmatrix}. \]
Hierarchical parameterisation
\[ y_{ijk} \sim N(\mu_{ij}, \sigma^2), \;\;\; \mu_{ij}= \beta_0 + \beta_i + \gamma_{j(i)}, \]
where \(\gamma_{ij} \sim N(0, \sigma^2_B)\), \(\beta_0, \beta_i \sim N(0, 1000000)\), and \(\sigma^2, \sigma^2_B \sim \text{Cauchy(0, 25)}\).
Rather than assume a specific variance-covariance structure, just like lme we can incorporate an appropriate structure to account for different dependency/correlation structures in our data. In RCB designs, it is prudent to capture the residuals to allow checks that there are no outstanding dependency issues following model fitting.
Full effect parameterisation
> modelString="
+ model {
+ #Likelihood
+ for (i in 1:n) {
+ y[i]~dnorm(mu[i],tau)
+ mu[i] <- beta0 + beta[A[i]] + gamma[Block[i]]
+ res[i] <- y[i]-mu[i]
+ }
+
+ #Priors
+ beta0 ~ dnorm(0, 1.0E-6)
+ beta[1] <- 0
+ for (i in 2:nA) {
+ beta[i] ~ dnorm(0, 1.0E-6) #prior
+ }
+ for (i in 1:nBlock) {
+ gamma[i] ~ dnorm(0, tau.B) #prior
+ }
+ tau <- pow(sigma,-2)
+ sigma <- z/sqrt(chSq)
+ z ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq ~ dgamma(0.5, 0.5)
+
+ tau.B <- pow(sigma.B,-2)
+ sigma.B <- z/sqrt(chSq.B)
+ z.B ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq.B ~ dgamma(0.5, 0.5)
+ }
+ "
>
> ## write the model to a text file
> writeLines(modelString, con = "fullModel.txt")Arrange the data as a list (as required by JAGS). As input, JAGS will need to be supplied with: the response variable, the predictor matrix, the number of predictors, the total number of observed items. This all needs to be contained within a list object. We will create two data lists, one for each of the hypotheses.
> data.rcb.list <- with(data.rcb,
+ list(y=y,
+ Block=as.numeric(Block),
+ A=as.numeric(A),
+ n=nrow(data.rcb),
+ nBlock=length(levels(Block)),
+ nA = length(levels(A))
+ )
+ )Define the nodes (parameters and derivatives) to monitor and the chain parameters.
> params <- c("beta0","beta",'gamma',"sigma","sigma.B","res")
> burnInSteps = 3000
> nChains = 2
> numSavedSteps = 3000
> thinSteps = 1
> nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains)Start the JAGS model (check the model, load data into the model, specify the number of chains and compile the model). Load the R2jags package.
> library(R2jags)Now run the JAGS code via the R2jags interface.
> data.rcb.r2jags.f <- jags(data = data.rcb.list, inits = NULL, parameters.to.save = params,
+ model.file = "fullModel.txt", n.chains = nChains, n.iter = nIter,
+ n.burnin = burnInSteps, n.thin = thinSteps)
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 105
Unobserved stochastic nodes: 42
Total graph size: 582
Initializing model
>
> print(data.rcb.r2jags.f)
Inference for Bugs model at "fullModel.txt", fit using jags,
2 chains, each with 4500 iterations (first 3000 discarded)
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta[1] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1.000 1
beta[2] 27.923 1.236 25.587 27.086 27.918 28.736 30.363 1.001 3000
beta[3] 40.263 1.229 37.821 39.463 40.271 41.070 42.706 1.001 3000
beta0 41.834 2.154 37.519 40.406 41.833 43.338 46.002 1.001 3000
gamma[1] 3.731 3.394 -2.865 1.418 3.748 6.043 10.452 1.001 3000
gamma[2] 4.534 3.439 -2.033 2.182 4.508 6.865 11.317 1.003 690
gamma[3] -3.951 3.464 -10.690 -6.324 -3.884 -1.600 2.829 1.001 3000
gamma[4] -4.129 3.454 -10.758 -6.477 -4.200 -1.784 2.630 1.003 780
gamma[5] -5.314 3.480 -12.143 -7.633 -5.325 -2.947 1.594 1.001 3000
gamma[6] -6.050 3.377 -12.486 -8.331 -6.071 -3.700 0.524 1.001 3000
gamma[7] -0.709 3.373 -7.083 -3.017 -0.728 1.585 6.032 1.001 3000
gamma[8] -15.033 3.446 -21.689 -17.322 -15.065 -12.741 -7.939 1.001 3000
gamma[9] 27.856 3.444 20.996 25.498 27.927 30.226 34.525 1.001 3000
gamma[10] 12.830 3.591 5.798 10.453 12.809 15.249 20.065 1.001 3000
gamma[11] -14.936 3.427 -21.825 -17.228 -14.945 -12.635 -8.165 1.001 3000
gamma[12] -7.878 3.427 -14.571 -10.161 -7.929 -5.551 -1.275 1.001 3000
gamma[13] -10.865 3.430 -17.569 -13.203 -10.852 -8.555 -4.076 1.001 2100
gamma[14] 9.153 3.466 2.557 6.679 9.161 11.473 15.941 1.002 1100
gamma[15] -3.897 3.495 -10.811 -6.227 -3.882 -1.565 2.866 1.001 3000
gamma[16] 1.321 3.437 -5.486 -0.927 1.328 3.539 8.066 1.001 3000
gamma[17] -4.137 3.445 -11.102 -6.451 -4.046 -1.802 2.384 1.001 2300
gamma[18] -4.257 3.449 -10.970 -6.607 -4.280 -1.978 2.695 1.001 2900
gamma[19] 16.435 3.468 9.749 14.031 16.449 18.830 23.059 1.002 1600
gamma[20] -5.108 3.439 -11.784 -7.392 -5.100 -2.851 1.708 1.001 3000
gamma[21] 18.935 3.517 12.023 16.632 18.857 21.210 25.944 1.001 3000
gamma[22] -20.654 3.459 -27.290 -23.041 -20.593 -18.341 -14.063 1.001 3000
gamma[23] 7.325 3.570 0.265 4.959 7.346 9.652 14.226 1.001 2500
gamma[24] -1.300 3.500 -8.248 -3.680 -1.256 1.043 5.590 1.001 3000
gamma[25] -6.114 3.419 -12.672 -8.442 -6.078 -3.725 0.554 1.001 2500
gamma[26] 1.038 3.451 -5.502 -1.351 1.018 3.415 7.820 1.001 3000
gamma[27] -4.346 3.400 -10.942 -6.604 -4.351 -1.980 2.254 1.001 3000
gamma[28] -4.721 3.368 -11.281 -6.939 -4.724 -2.572 2.057 1.001 3000
gamma[29] -12.328 3.513 -19.166 -14.660 -12.295 -10.096 -5.361 1.001 3000
gamma[30] -12.858 3.534 -19.927 -15.216 -12.782 -10.455 -5.999 1.001 3000
gamma[31] 0.272 3.457 -6.677 -2.020 0.279 2.562 7.061 1.002 1700
gamma[32] 8.682 3.389 1.905 6.358 8.769 10.986 15.304 1.002 1100
gamma[33] 0.315 3.433 -6.393 -2.013 0.292 2.624 7.101 1.001 3000
gamma[34] 9.586 3.491 2.775 7.232 9.621 11.954 16.438 1.002 1600
gamma[35] 23.906 3.429 17.230 21.620 23.976 26.208 30.709 1.004 660
res[1] 0.243 2.906 -5.276 -1.686 0.233 2.121 5.940 1.001 3000
res[2] -6.771 2.869 -12.345 -8.647 -6.778 -4.904 -1.088 1.001 3000
res[3] 7.465 2.940 1.587 5.472 7.482 9.382 13.252 1.001 3000
res[4] -3.267 2.927 -8.857 -5.249 -3.282 -1.245 2.325 1.003 710
res[5] -1.085 2.946 -6.792 -3.130 -1.110 0.894 4.685 1.003 580
res[6] 5.144 2.913 -0.568 3.244 5.128 7.112 11.094 1.003 600
res[7] -0.049 2.992 -5.806 -2.023 -0.081 1.917 5.915 1.002 1400
res[8] -2.652 3.020 -8.617 -4.629 -2.690 -0.658 3.254 1.001 2100
res[9] 2.018 2.992 -3.965 -0.008 1.989 4.022 7.816 1.001 1900
res[10] -2.071 2.894 -7.884 -4.016 -2.075 -0.143 3.626 1.003 790
res[11] 0.729 2.960 -5.122 -1.274 0.754 2.666 6.590 1.003 660
res[12] 0.287 2.974 -5.811 -1.700 0.396 2.232 5.977 1.003 700
res[13] -2.939 2.956 -8.894 -4.938 -2.989 -0.959 2.831 1.001 3000
res[14] 4.213 2.943 -1.578 2.254 4.220 6.162 10.013 1.002 3000
res[15] -2.451 2.949 -8.246 -4.449 -2.478 -0.503 3.535 1.001 3000
res[16] -2.462 2.911 -8.169 -4.429 -2.422 -0.560 3.167 1.001 3000
res[17] 3.440 2.912 -2.164 1.559 3.394 5.390 9.051 1.001 3000
res[18] -2.208 2.908 -7.897 -4.117 -2.183 -0.279 3.505 1.001 3000
res[19] -5.249 2.902 -10.958 -7.149 -5.263 -3.289 0.456 1.001 2800
res[20] 4.201 2.886 -1.484 2.238 4.217 6.100 9.930 1.001 3000
res[21] 1.085 2.889 -4.579 -0.852 1.104 2.988 6.981 1.001 3000
res[22] 0.756 2.958 -5.385 -1.108 0.712 2.747 6.541 1.001 3000
res[23] 1.284 2.979 -4.882 -0.642 1.295 3.319 6.941 1.001 3000
res[24] -5.388 2.941 -11.391 -7.320 -5.410 -3.425 0.336 1.001 3000
res[25] 3.141 2.979 -2.786 1.153 3.135 5.090 9.051 1.001 3000
res[26] -4.587 2.978 -10.372 -6.597 -4.605 -2.589 1.268 1.001 3000
res[27] 7.011 2.963 1.359 4.983 6.994 8.965 12.803 1.001 3000
res[28] 7.495 3.018 1.549 5.443 7.508 9.538 13.331 1.002 1600
res[29] 0.730 3.013 -5.133 -1.311 0.723 2.759 6.603 1.001 2200
res[30] -5.563 3.054 -11.597 -7.683 -5.577 -3.452 0.255 1.001 2100
res[31] -3.927 2.962 -9.656 -5.903 -3.900 -1.965 1.925 1.001 3000
res[32] 2.986 2.928 -2.794 1.134 2.985 4.946 8.735 1.001 3000
res[33] -1.871 2.951 -7.734 -3.824 -1.864 0.076 4.020 1.001 3000
res[34] -0.528 2.951 -6.322 -2.505 -0.516 1.395 5.205 1.001 3000
res[35] -1.472 2.949 -7.285 -3.350 -1.439 0.455 4.220 1.001 3000
res[36] 0.722 2.938 -4.922 -1.223 0.716 2.663 6.487 1.001 3000
res[37] -0.493 2.928 -6.329 -2.503 -0.515 1.546 5.111 1.002 940
res[38] -2.832 2.938 -8.610 -4.822 -2.827 -0.812 2.778 1.002 1300
res[39] 1.268 2.931 -4.339 -0.752 1.281 3.287 6.896 1.002 1200
res[40] 2.968 2.956 -2.952 0.972 2.987 4.925 8.768 1.003 540
res[41] -2.427 2.942 -8.293 -4.383 -2.363 -0.534 3.629 1.003 660
res[42] 1.150 2.922 -4.453 -0.813 1.176 3.054 7.197 1.003 620
res[43] -7.026 2.953 -12.859 -8.930 -7.097 -5.036 -1.170 1.001 3000
res[44] 2.862 2.915 -2.600 0.922 2.711 4.854 8.438 1.001 3000
res[45] 3.397 2.955 -2.273 1.404 3.364 5.361 9.127 1.001 3000
res[46] 1.390 2.972 -4.597 -0.607 1.321 3.366 7.167 1.001 2000
res[47] 2.490 2.991 -3.362 0.502 2.495 4.531 8.375 1.001 3000
res[48] -3.582 2.963 -9.351 -5.573 -3.608 -1.606 2.286 1.001 2700
res[49] -2.288 2.916 -7.729 -4.298 -2.366 -0.291 3.588 1.003 1000
res[50] -1.083 2.906 -6.569 -3.067 -1.105 0.863 4.716 1.002 1300
res[51] 2.286 2.912 -3.216 0.331 2.244 4.222 8.075 1.002 1200
res[52] -2.829 2.903 -8.540 -4.796 -2.804 -0.891 2.706 1.001 3000
res[53] 1.533 2.928 -4.178 -0.380 1.544 3.452 7.214 1.001 2700
res[54] 0.366 2.907 -5.326 -1.576 0.391 2.274 6.016 1.001 3000
res[55] 7.373 2.957 1.529 5.353 7.414 9.358 13.176 1.002 1300
res[56] -3.029 2.984 -9.041 -4.985 -2.963 -1.047 2.888 1.002 1000
res[57] -0.932 2.961 -6.889 -2.936 -0.824 0.995 4.741 1.002 1100
res[58] 0.955 2.941 -4.752 -1.089 0.981 2.907 6.650 1.001 3000
res[59] -2.168 2.938 -8.052 -4.106 -2.164 -0.262 3.668 1.001 3000
res[60] -0.054 2.957 -5.874 -2.011 0.024 1.879 5.755 1.001 3000
res[61] 4.652 3.013 -1.277 2.681 4.595 6.649 10.447 1.001 3000
res[62] 1.763 3.015 -4.198 -0.283 1.800 3.811 7.690 1.001 3000
res[63] -2.627 2.975 -8.515 -4.603 -2.640 -0.650 3.124 1.001 3000
res[64] -1.878 3.019 -7.923 -3.808 -1.879 0.207 3.832 1.001 3000
res[65] -7.955 2.986 -14.124 -9.906 -7.908 -5.914 -2.185 1.001 3000
res[66] 5.629 3.022 -0.370 3.651 5.702 7.692 11.441 1.001 3000
res[67] -9.447 2.997 -15.297 -11.427 -9.472 -7.515 -3.360 1.002 1100
res[68] 3.633 3.011 -2.241 1.639 3.558 5.638 9.647 1.002 1400
res[69] 7.139 3.005 1.189 5.081 7.118 9.082 13.136 1.002 1300
res[70] -6.267 2.959 -11.956 -8.323 -6.249 -4.253 -0.493 1.001 3000
res[71] 6.538 2.978 0.563 4.494 6.525 8.512 12.391 1.001 3000
res[72] -0.621 2.967 -6.432 -2.609 -0.683 1.364 5.125 1.001 3000
res[73] -0.989 2.943 -6.875 -2.968 -0.975 0.949 4.951 1.001 3000
res[74] 1.375 2.946 -4.265 -0.614 1.336 3.269 7.187 1.001 2400
res[75] -1.399 2.934 -7.135 -3.371 -1.401 0.618 4.478 1.001 2700
res[76] -0.971 2.970 -6.912 -2.914 -1.004 1.027 4.841 1.001 3000
res[77] -3.549 2.958 -9.315 -5.540 -3.567 -1.572 2.143 1.001 3000
res[78] 4.860 2.940 -0.988 2.887 4.805 6.835 10.606 1.001 3000
res[79] 6.984 2.964 1.461 4.967 6.920 9.004 12.824 1.001 3000
res[80] -7.875 3.011 -13.687 -9.926 -7.936 -5.815 -1.954 1.001 3000
res[81] 0.160 2.947 -5.484 -1.824 0.127 2.155 6.047 1.001 3000
res[82] 2.734 2.915 -3.183 0.820 2.794 4.729 8.263 1.001 3000
res[83] 2.626 2.932 -3.161 0.748 2.624 4.515 8.266 1.001 3000
res[84] -6.416 2.954 -12.297 -8.315 -6.382 -4.439 -0.826 1.001 3000
res[85] -2.326 3.020 -8.242 -4.293 -2.308 -0.307 3.564 1.001 3000
res[86] -1.054 3.030 -7.047 -3.116 -1.048 0.971 4.956 1.001 3000
res[87] 0.823 3.034 -5.036 -1.236 0.832 2.846 6.820 1.001 3000
res[88] -3.700 3.021 -9.662 -5.732 -3.744 -1.656 2.141 1.001 3000
res[89] 5.124 3.000 -0.700 3.125 5.166 7.053 10.967 1.001 3000
res[90] -3.973 3.026 -9.965 -5.967 -3.979 -1.965 2.004 1.001 3000
res[91] 6.800 2.936 1.114 4.888 6.726 8.792 12.683 1.001 2100
res[92] -1.633 2.932 -7.382 -3.615 -1.645 0.303 4.342 1.002 1500
res[93] -5.027 2.937 -10.801 -6.975 -5.090 -3.114 0.895 1.002 1600
res[94] 11.068 2.894 5.415 9.144 11.037 12.950 16.844 1.017 920
res[95] -5.145 2.871 -10.758 -7.025 -5.209 -3.257 0.653 1.002 920
res[96] -3.909 2.889 -9.670 -5.821 -3.975 -2.083 2.104 1.002 1000
res[97] 1.670 2.927 -4.070 -0.286 1.655 3.647 7.528 1.001 2600
res[98] -1.855 2.902 -7.533 -3.814 -1.846 0.085 3.932 1.001 3000
res[99] 0.809 2.905 -4.984 -1.113 0.807 2.832 6.509 1.001 3000
res[100] 1.492 2.952 -4.294 -0.488 1.451 3.471 7.192 1.001 2000
res[101] 0.647 2.987 -5.287 -1.341 0.649 2.697 6.465 1.002 1500
res[102] -0.289 2.974 -6.080 -2.262 -0.296 1.781 5.395 1.002 1600
res[103] -1.309 2.976 -7.063 -3.273 -1.394 0.728 4.790 1.004 440
res[104] 11.580 2.959 5.725 9.638 11.567 13.515 17.434 1.003 770
res[105] -5.108 2.939 -10.788 -7.110 -5.108 -3.165 0.707 1.006 490
sigma 5.090 0.453 4.294 4.775 5.059 5.360 6.091 1.002 980
sigma.B 11.494 1.491 8.926 10.487 11.365 12.348 14.912 1.002 920
deviance 637.702 11.556 618.449 629.190 636.668 645.140 663.417 1.001 3000
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 66.8 and DIC = 704.5
DIC is an estimate of expected predictive error (lower deviance is better).Matrix parameterisation
> modelString2="
+ model {
+ #Likelihood
+ for (i in 1:n) {
+ y[i]~dnorm(mu[i],tau)
+ mu[i] <- inprod(beta[],X[i,]) + gamma[Block[i]]
+ res[i] <- y[i]-mu[i]
+ }
+
+ #Priors
+ beta ~ dmnorm(a0,A0)
+ for (i in 1:nBlock) {
+ gamma[i] ~ dnorm(0, tau.B) #prior
+ }
+ tau <- pow(sigma,-2)
+ sigma <- z/sqrt(chSq)
+ z ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq ~ dgamma(0.5, 0.5)
+
+ tau.B <- pow(sigma.B,-2)
+ sigma.B <- z/sqrt(chSq.B)
+ z.B ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq.B ~ dgamma(0.5, 0.5)
+ }
+ "
>
> ## write the model to a text file
> writeLines(modelString2, con = "matrixModel.txt")Arrange the data as a list (as required by JAGS). As input, JAGS will need to be supplied with: the response variable, the predictor matrix, the number of predictors, the total number of observed items. This all needs to be contained within a list object. We will create two data lists, one for each of the hypotheses.
> A.Xmat <- model.matrix(~A,data.rcb)
> data.rcb.list <- with(data.rcb,
+ list(y=y,
+ Block=as.numeric(Block),
+ X=A.Xmat,
+ n=nrow(data.rcb),
+ nBlock=length(levels(Block)),
+ a0=rep(0,3), A0=diag(3)
+ )
+ )Define the nodes (parameters and derivatives) to monitor and the chain parameters.
> params <- c("beta",'gamma',"sigma","sigma.B","res")
> adaptSteps = 1000
> burnInSteps = 3000
> nChains = 2
> numSavedSteps = 3000
> thinSteps = 1
> nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains)Now run the JAGS code via the R2jags interface.
> data.rcb.r2jags.m <- jags(data = data.rcb.list, inits = NULL, parameters.to.save = params,
+ model.file = "matrixModel.txt", n.chains = nChains, n.iter = nIter,
+ n.burnin = burnInSteps, n.thin = thinSteps)
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 105
Unobserved stochastic nodes: 40
Total graph size: 910
Initializing model
>
> print(data.rcb.r2jags.m)
Inference for Bugs model at "matrixModel.txt", fit using jags,
2 chains, each with 4500 iterations (first 3000 discarded)
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta[1] 0.550 1.010 -1.396 -0.163 0.543 1.212 2.618 1.001 3000
beta[2] 0.624 0.969 -1.267 -0.021 0.609 1.267 2.494 1.002 830
beta[3] 1.556 1.005 -0.458 0.886 1.564 2.248 3.495 1.001 3000
gamma[1] 64.957 12.115 41.593 56.722 64.856 72.937 89.019 1.001 3000
gamma[2] 65.491 12.061 40.343 57.573 65.450 73.443 89.230 1.001 3000
gamma[3] 57.107 11.937 34.004 49.204 56.969 65.191 79.840 1.001 3000
gamma[4] 56.660 11.705 32.676 48.922 56.796 64.418 79.244 1.002 980
gamma[5] 55.496 12.269 30.868 47.463 55.494 63.576 79.632 1.001 3000
gamma[6] 54.801 11.877 31.954 46.951 54.385 62.674 78.056 1.002 3000
gamma[7] 60.234 11.740 36.788 52.823 60.472 67.916 83.053 1.001 3000
gamma[8] 45.171 11.789 21.628 37.438 45.279 53.104 69.031 1.002 3000
gamma[9] 89.740 11.870 66.877 81.784 89.985 97.893 112.876 1.001 3000
gamma[10] 74.392 11.959 51.486 65.937 74.289 82.703 98.386 1.002 1500
gamma[11] 45.824 11.994 22.631 37.864 45.861 53.737 69.411 1.002 1100
gamma[12] 52.874 11.847 29.777 44.934 53.044 61.009 75.635 1.002 1800
gamma[13] 49.828 12.010 26.670 41.934 49.809 57.903 73.611 1.001 3000
gamma[14] 70.252 11.879 46.842 62.471 70.259 78.152 93.618 1.001 3000
gamma[15] 56.956 11.790 34.318 48.968 56.782 65.102 79.771 1.001 3000
gamma[16] 62.229 12.088 39.561 53.779 62.120 70.801 85.754 1.002 1500
gamma[17] 56.154 11.923 32.379 48.260 56.301 64.248 79.156 1.004 840
gamma[18] 56.302 11.789 32.839 48.585 56.477 64.399 79.221 1.001 3000
gamma[19] 78.011 12.127 53.246 69.932 78.041 86.393 100.917 1.001 3000
gamma[20] 55.445 11.822 32.414 47.480 55.477 63.566 78.456 1.002 3000
gamma[21] 79.975 11.935 56.573 72.184 80.069 87.728 103.091 1.001 3000
gamma[22] 39.667 11.800 16.288 31.836 39.723 47.341 62.882 1.001 3000
gamma[23] 68.605 11.860 45.831 60.540 68.721 76.702 91.376 1.001 3000
gamma[24] 59.858 12.057 36.038 51.799 59.900 67.940 83.312 1.001 2200
gamma[25] 54.974 11.970 31.161 47.135 55.153 62.882 78.327 1.002 1400
gamma[26] 62.397 11.915 38.745 54.113 62.260 70.437 86.239 1.002 3000
gamma[27] 56.526 11.968 32.943 48.610 56.627 64.491 80.067 1.003 1800
gamma[28] 56.062 12.002 33.315 48.254 56.158 64.016 79.264 1.001 3000
gamma[29] 47.976 11.787 24.940 39.984 47.840 55.752 71.140 1.001 3000
gamma[30] 47.866 11.894 24.408 40.161 47.877 55.955 70.787 1.001 3000
gamma[31] 61.528 12.021 37.815 53.617 61.620 69.800 84.596 1.001 3000
gamma[32] 70.047 11.805 46.872 62.230 70.224 78.030 93.180 1.001 3000
gamma[33] 61.830 11.934 38.654 53.718 61.828 69.563 85.450 1.002 1800
gamma[34] 70.909 12.075 47.408 62.788 70.805 78.794 95.338 1.002 3000
gamma[35] 85.532 12.138 61.716 77.422 85.479 93.434 109.336 1.001 3000
res[1] -19.698 12.037 -43.684 -27.635 -19.684 -11.694 3.838 1.001 3000
res[2] 0.587 12.062 -23.374 -7.403 0.579 8.638 24.005 1.001 2500
res[3] 26.230 12.050 2.155 18.315 26.057 34.356 50.024 1.001 3000
res[4] -22.940 11.997 -46.569 -30.787 -23.060 -15.111 2.226 1.001 3000
res[5] 6.542 11.989 -16.855 -1.311 6.542 14.381 31.699 1.001 3000
res[6] 24.179 11.977 0.862 16.176 24.040 31.902 49.149 1.001 3000
res[7] -19.824 11.904 -42.484 -27.853 -19.648 -11.889 3.474 1.001 3000
res[8] 4.872 11.923 -17.801 -3.160 4.933 12.798 28.368 1.001 3000
res[9] 20.951 11.893 -1.904 12.827 21.045 28.785 44.008 1.001 3000
res[10] -21.576 11.660 -44.079 -29.235 -21.708 -13.770 2.548 1.002 920
res[11] 8.523 11.658 -14.011 0.830 8.435 16.332 32.472 1.002 1100
res[12] 19.489 11.657 -2.829 11.774 19.266 27.343 43.385 1.002 910
res[13] -22.465 12.167 -46.486 -30.516 -22.434 -14.565 2.114 1.001 3000
res[14] 11.986 12.183 -11.847 3.842 12.016 20.032 36.714 1.001 3000
res[15] 16.730 12.218 -7.281 8.522 16.737 24.706 41.406 1.001 3000
res[16] -22.029 11.845 -45.221 -29.925 -21.621 -14.244 0.444 1.001 3000
res[17] 11.172 11.874 -12.338 3.326 11.433 18.964 33.977 1.001 3000
res[18] 16.933 11.886 -6.385 8.941 17.228 24.796 39.651 1.001 3000
res[19] -24.908 11.723 -47.784 -32.552 -25.170 -17.491 -1.875 1.001 3000
res[20] 11.841 11.745 -11.265 4.268 11.662 19.369 35.065 1.001 3000
res[21] 20.133 11.744 -2.743 12.424 19.956 27.740 43.426 1.001 3000
res[22] -18.164 11.729 -41.484 -26.023 -18.365 -10.358 5.425 1.001 3000
res[23] 9.664 11.740 -13.656 1.865 9.491 17.451 33.025 1.001 3000
res[24] 14.399 11.768 -8.920 6.550 14.224 22.160 38.381 1.001 3000
res[25] -17.459 11.814 -40.240 -25.508 -17.731 -9.597 5.503 1.001 3000
res[26] 2.112 11.834 -20.695 -5.859 1.791 9.903 25.291 1.001 3000
res[27] 25.119 11.869 2.237 17.073 24.856 33.014 48.190 1.001 3000
res[28] -12.783 11.927 -36.486 -21.081 -12.685 -4.484 10.101 1.002 1600
res[29] 7.751 11.951 -16.443 -0.606 7.820 16.063 30.397 1.001 2100
res[30] 12.866 11.971 -10.922 4.637 12.799 21.163 36.114 1.002 1600
res[31] -23.404 11.959 -47.054 -31.381 -23.430 -15.471 -0.221 1.002 1200
res[32] 10.809 11.960 -12.765 2.757 10.883 18.657 33.990 1.002 1400
res[33] 17.359 11.972 -6.134 9.343 17.364 25.293 40.617 1.002 1100
res[34] -19.997 11.800 -42.736 -28.106 -20.202 -12.124 3.343 1.002 2500
res[35] 6.359 11.812 -16.232 -1.893 6.081 14.115 29.804 1.002 1900
res[36] 19.960 11.807 -2.519 11.753 19.730 27.900 43.458 1.002 2600
res[37] -19.902 11.980 -43.600 -27.871 -19.843 -12.058 3.587 1.001 3000
res[38] 5.059 12.005 -18.429 -3.025 5.164 12.756 28.837 1.001 3000
res[39] 20.566 11.996 -3.070 12.608 20.634 28.366 44.009 1.001 3000
res[40] -16.847 11.831 -39.884 -24.766 -17.012 -9.239 6.596 1.001 3000
res[41] 5.057 11.855 -18.074 -2.883 4.927 12.687 28.394 1.001 3000
res[42] 20.042 11.830 -3.241 12.206 20.003 27.718 43.766 1.001 3000
res[43] -26.596 11.746 -49.680 -34.580 -26.349 -18.627 -3.862 1.001 3000
res[44] 10.592 11.735 -12.047 2.531 10.659 18.547 33.288 1.001 3000
res[45] 22.535 11.759 -0.427 14.411 22.577 30.481 45.274 1.001 3000
res[46] -18.234 12.031 -41.669 -26.696 -18.076 -9.978 4.443 1.002 1200
res[47] 10.165 12.061 -13.282 1.662 10.365 18.474 33.054 1.002 1500
res[48] 15.501 12.060 -7.938 7.051 15.690 23.578 38.325 1.002 1200
res[49] -21.296 11.891 -44.247 -29.499 -21.509 -13.441 2.004 1.002 1000
res[50] 7.208 11.902 -15.618 -0.939 6.981 15.152 30.441 1.002 860
res[51] 21.986 11.895 -0.592 13.867 21.799 29.853 45.640 1.002 1000
res[52] -22.104 11.729 -44.941 -29.987 -22.312 -14.241 1.133 1.001 3000
res[53] 9.556 11.751 -13.024 1.751 9.257 17.457 33.011 1.001 3000
res[54] 19.797 11.734 -2.966 11.838 19.629 27.542 43.295 1.001 3000
res[55] -12.918 12.097 -35.949 -21.363 -12.982 -4.866 11.578 1.001 3000
res[56] 3.979 12.106 -19.166 -4.374 3.889 12.063 28.610 1.001 3000
res[57] 17.484 12.122 -5.688 8.981 17.300 25.557 42.114 1.001 3000
res[58] -18.315 11.797 -41.135 -26.620 -18.209 -10.520 4.471 1.001 3000
res[59] 5.862 11.815 -16.900 -2.341 6.146 13.803 29.023 1.001 3000
res[60] 19.383 11.783 -3.464 11.144 19.447 27.072 42.559 1.001 3000
res[61] -15.105 11.900 -38.125 -22.888 -15.284 -7.276 8.233 1.001 3000
res[62] 9.306 11.923 -13.585 1.507 9.128 17.140 32.775 1.001 3000
res[63] 16.323 11.956 -6.322 8.357 16.116 24.316 39.779 1.001 3000
res[64] -20.915 11.793 -44.085 -28.598 -21.048 -13.147 2.444 1.001 3000
res[65] 0.307 11.820 -22.750 -7.598 0.334 7.975 23.864 1.001 3000
res[66] 25.298 11.813 2.156 17.551 25.247 33.151 48.893 1.001 3000
res[67] -29.443 11.830 -52.213 -37.430 -29.692 -21.434 -6.575 1.001 3000
res[68] 10.936 11.848 -11.706 2.810 10.811 18.885 33.881 1.001 3000
res[69] 25.850 11.873 2.835 17.722 25.645 33.821 48.845 1.001 3000
res[70] -26.142 11.991 -49.697 -34.072 -26.243 -18.049 -2.711 1.001 2300
res[71] 13.963 11.984 -9.101 6.160 13.990 22.029 37.049 1.001 3000
res[72] 18.211 12.015 -4.983 10.314 18.104 26.258 41.685 1.001 2300
res[73] -20.794 11.932 -43.963 -28.725 -20.938 -12.958 3.106 1.002 1600
res[74] 8.870 11.937 -14.459 0.895 8.787 16.905 32.822 1.001 2000
res[75] 17.504 11.929 -5.274 9.402 17.317 25.457 41.765 1.002 1600
res[76] -21.046 11.851 -44.910 -28.922 -21.131 -12.843 2.003 1.002 3000
res[77] 3.675 11.857 -19.985 -4.059 3.613 11.706 27.196 1.003 3000
res[78] 23.492 11.881 -0.028 15.552 23.399 31.576 46.776 1.003 3000
res[79] -12.603 11.937 -35.961 -20.361 -12.719 -4.579 10.948 1.002 2900
res[80] -0.163 11.955 -23.303 -8.120 -0.343 7.789 23.405 1.002 2200
res[81] 19.279 11.963 -4.001 11.319 19.160 27.293 42.755 1.002 3000
res[82] -16.766 11.961 -39.955 -24.721 -16.887 -9.030 6.016 1.001 3000
res[83] 10.426 11.958 -13.000 2.504 10.510 18.221 32.859 1.001 3000
res[84] 12.792 11.939 -10.192 4.873 12.720 20.537 35.661 1.001 3000
res[85] -21.347 11.725 -44.125 -28.923 -21.164 -13.609 1.848 1.001 3000
res[86] 7.224 11.690 -15.758 -0.362 7.382 15.079 30.544 1.001 3000
res[87] 20.510 11.739 -2.412 12.708 20.647 28.327 43.283 1.001 3000
res[88] -23.140 11.838 -46.005 -31.274 -23.099 -15.502 -0.066 1.001 3000
res[89] 12.983 11.858 -9.972 4.729 13.009 20.680 36.860 1.001 3000
res[90] 15.293 11.892 -7.122 6.928 15.405 23.032 38.696 1.001 3000
res[91] -13.173 11.935 -36.126 -21.376 -13.267 -5.416 10.293 1.001 3000
res[92] 5.694 11.935 -17.082 -2.485 5.640 13.450 29.247 1.001 3000
res[93] 13.708 11.936 -9.020 5.488 13.624 21.589 37.402 1.001 3000
res[94] -9.013 11.766 -31.685 -16.863 -9.233 -1.091 14.418 1.001 3000
res[95] 2.073 11.780 -20.569 -5.756 1.871 9.830 25.639 1.001 3000
res[96] 14.717 11.782 -8.181 6.737 14.422 22.602 37.767 1.001 3000
res[97] -18.561 11.906 -41.914 -26.360 -18.779 -10.492 4.073 1.002 1300
res[98] 5.213 11.908 -18.272 -2.559 5.068 13.190 28.414 1.002 1100
res[99] 19.285 11.939 -4.469 11.483 19.203 27.469 42.441 1.002 1300
res[100] -18.547 12.018 -42.274 -26.484 -18.430 -10.631 5.083 1.001 3000
res[101] 7.907 12.020 -16.041 -0.084 8.072 15.733 31.471 1.001 3000
res[102] 18.379 12.034 -5.679 10.333 18.514 26.429 41.930 1.001 3000
res[103] -21.652 12.104 -45.310 -29.603 -21.605 -13.692 1.709 1.001 2500
res[104] 18.537 12.095 -5.105 10.797 18.645 26.404 42.117 1.001 1900
res[105] 13.256 12.137 -10.949 5.489 13.253 21.341 36.897 1.001 2600
sigma 20.838 1.809 17.597 19.556 20.736 21.936 24.751 1.002 1000
sigma.B 63.500 7.812 50.201 58.005 62.978 68.138 80.806 1.001 3000
deviance 934.350 11.459 914.767 926.442 933.465 941.520 959.367 1.004 460
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 65.5 and DIC = 999.9
DIC is an estimate of expected predictive error (lower deviance is better).For a simple model with only two hierarchical levels, the model is the same as above. If you want to include finite-population standard deviations in the model you can use the following code.
> modelString3="
+ model {
+ #Likelihood (esimating site means (gamma.site)
+ for (i in 1:n) {
+ y[i]~dnorm(mu[i],tau)
+ mu[i] <- gamma[Block[i]] + inprod(beta[], X[i,])
+ y.err[i]<- mu[i]-y[i]
+ }
+ for (i in 1:nBlock) {
+ gamma[i] ~ dnorm(0, tau.block)
+ }
+ #Priors
+ for (i in 1:nX) {
+ beta[i] ~ dnorm(0, 1.0E-6) #prior
+ }
+ sigma ~ dunif(0, 100)
+ tau <- 1 / (sigma * sigma)
+ sigma.block ~ dunif(0, 100)
+ tau.block <- 1 / (sigma.block * sigma.block)
+
+ sd.y <- sd(y.err)
+ sd.block <- sd(gamma)
+ }
+ "
>
> ## write the model to a text file
> writeLines(modelString3, con = "SDModel.txt")
>
> #data list
> A.Xmat <- model.matrix(~A,ddply(data.rcb,~Block,catcolwise(unique)))
> data.rcb.list <- with(data.rcb,
+ list(y=y,
+ Block=Block,
+ X= A.Xmat,
+ n=nrow(data.rcb),
+ nBlock=length(levels(Block)),
+ nX = ncol(A.Xmat)
+ )
+ )
>
> #parameters and chain details
> params <- c("beta","sigma","sd.y",'sd.block','sigma.block')
> burnInSteps = 3000
> nChains = 2
> numSavedSteps = 3000
> thinSteps = 1
> nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains)
>
> data.rcb.r2jagsSD <- jags(data = data.rcb.list, inits = NULL, parameters.to.save = params,
+ model.file = "SDModel.txt", n.chains = nChains, n.iter = nIter,
+ n.burnin = burnInSteps, n.thin = thinSteps)
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 105
Unobserved stochastic nodes: 40
Total graph size: 899
Initializing model
>
> print(data.rcb.r2jagsSD)
Inference for Bugs model at "SDModel.txt", fit using jags,
2 chains, each with 4500 iterations (first 3000 discarded)
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat n.eff
beta[1] 41.715 2.196 37.449 40.231 41.710 43.183 45.995 1.001 3000
beta[2] 27.928 1.209 25.537 27.146 27.918 28.713 30.317 1.002 980
beta[3] 40.272 1.210 37.832 39.461 40.267 41.096 42.658 1.001 2300
sd.block 11.358 0.519 10.353 11.029 11.345 11.706 12.370 1.001 3000
sd.y 5.014 0.260 4.592 4.827 4.986 5.172 5.609 1.002 1300
sigma 5.074 0.443 4.322 4.752 5.045 5.350 6.036 1.001 3000
sigma.block 11.692 1.546 9.114 10.589 11.586 12.612 15.118 1.002 3000
deviance 637.262 10.949 618.392 629.413 636.321 644.252 660.930 1.001 2200
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 59.9 and DIC = 697.2
DIC is an estimate of expected predictive error (lower deviance is better).Calculate \(R^2\) from the posterior of the model.
> data.rcb.mcmc.listSD <- as.mcmc(data.rcb.r2jagsSD)
>
> Xmat <- model.matrix(~A, data.rcb)
> coefs <- data.rcb.r2jagsSD$BUGSoutput$sims.list[['beta']]
> fitted <- coefs %*% t(Xmat)
> X.var <- aaply(fitted,1,function(x){var(x)})
> Z.var <- data.rcb.r2jagsSD$BUGSoutput$sims.list[['sd.block']]^2
> R.var <- data.rcb.r2jagsSD$BUGSoutput$sims.list[['sd.y']]^2
> R2.marginal <- (X.var)/(X.var+Z.var+R.var)
> R2.marginal <- data.frame(Mean=mean(R2.marginal), Median=median(R2.marginal), HPDinterval(as.mcmc(R2.marginal)))
> R2.conditional <- (X.var+Z.var)/(X.var+Z.var+R.var)
> R2.conditional <- data.frame(Mean=mean(R2.conditional),
+ Median=median(R2.conditional), HPDinterval(as.mcmc(R2.conditional)))
> R2.block <- (Z.var)/(X.var+Z.var+R.var)
> R2.block <- data.frame(Mean=mean(R2.block), Median=median(R2.block), HPDinterval(as.mcmc(R2.block)))
> R2.res<-(R.var)/(X.var+Z.var+R.var)
> R2.res <- data.frame(Mean=mean(R2.res), Median=median(R2.res), HPDinterval(as.mcmc(R2.res)))
>
> rbind(R2.block=R2.block, R2.marginal=R2.marginal, R2.res=R2.res, R2.conditional=R2.conditional)
Mean Median lower upper
R2.block 0.2927774 0.29248056 0.24902731 0.33605200
R2.marginal 0.6500204 0.65101312 0.60509352 0.68965593
R2.res 0.0572022 0.05628758 0.04596228 0.07055798
R2.conditional 0.9427978 0.94371242 0.92944202 0.95403772Planned comparisonsand pairwise tests
Since there are no restrictions on the type and number of comparisons derived from the posteriors, Bayesian analyses provide a natural framework for exploring additional contrasts and comparisons. For example, to compare all possible levels:
> coefs <- data.rcb.r2jags.m$BUGSoutput$sims.list[[c('beta')]]
> head(coefs)
[,1] [,2] [,3]
[1,] -1.0697767 -0.46647636 0.4808020
[2,] 0.6186153 1.46210386 2.3592529
[3,] -1.5100302 0.09180824 1.1835869
[4,] -0.3127107 0.66392714 -0.5681012
[5,] 1.5552936 1.06785499 2.6443403
[6,] 0.7282182 0.59829747 2.8548669
>
> newdata <- data.frame(A=levels(data.rcb$A))
> # A Tukeys contrast matrix
> library(multcomp)
> tuk.mat <- contrMat(n=table(newdata$A), type="Tukey")
> Xmat <- model.matrix(~A, data=newdata)
> pairwise.mat <- tuk.mat %*% Xmat
> pairwise.mat
(Intercept) A2 A3
2 - 1 0 1 0
3 - 1 0 0 1
3 - 2 0 -1 1
>
> comps <- coefs %*% t(pairwise.mat)
>
> MCMCsum <- function(x) {
+ data.frame(Median=median(x, na.rm=TRUE), t(quantile(x,na.rm=TRUE)),
+ HPDinterval(as.mcmc(x)),HPDinterval(as.mcmc(x),p=0.5))
+ }
>
> (comps <-plyr:::adply(comps,2,MCMCsum))
X1 Median X0. X25. X50. X75. X100. lower
1 2 - 1 0.6093838 -2.556240 -0.020575421 0.6093838 1.267051 4.786166 -1.2766747
2 3 - 1 1.5638199 -1.833977 0.886430287 1.5638199 2.248195 4.835948 -0.4024791
3 3 - 2 0.9310770 -4.672228 -0.003765539 0.9310770 1.864871 5.592247 -1.5970184
upper lower.1 upper.1
1 2.479999 0.03512204 1.316762
2 3.539364 0.92897200 2.273364
3 3.728297 -0.03345687 1.823124RCB (repeated measures) - continuous within
Data generation
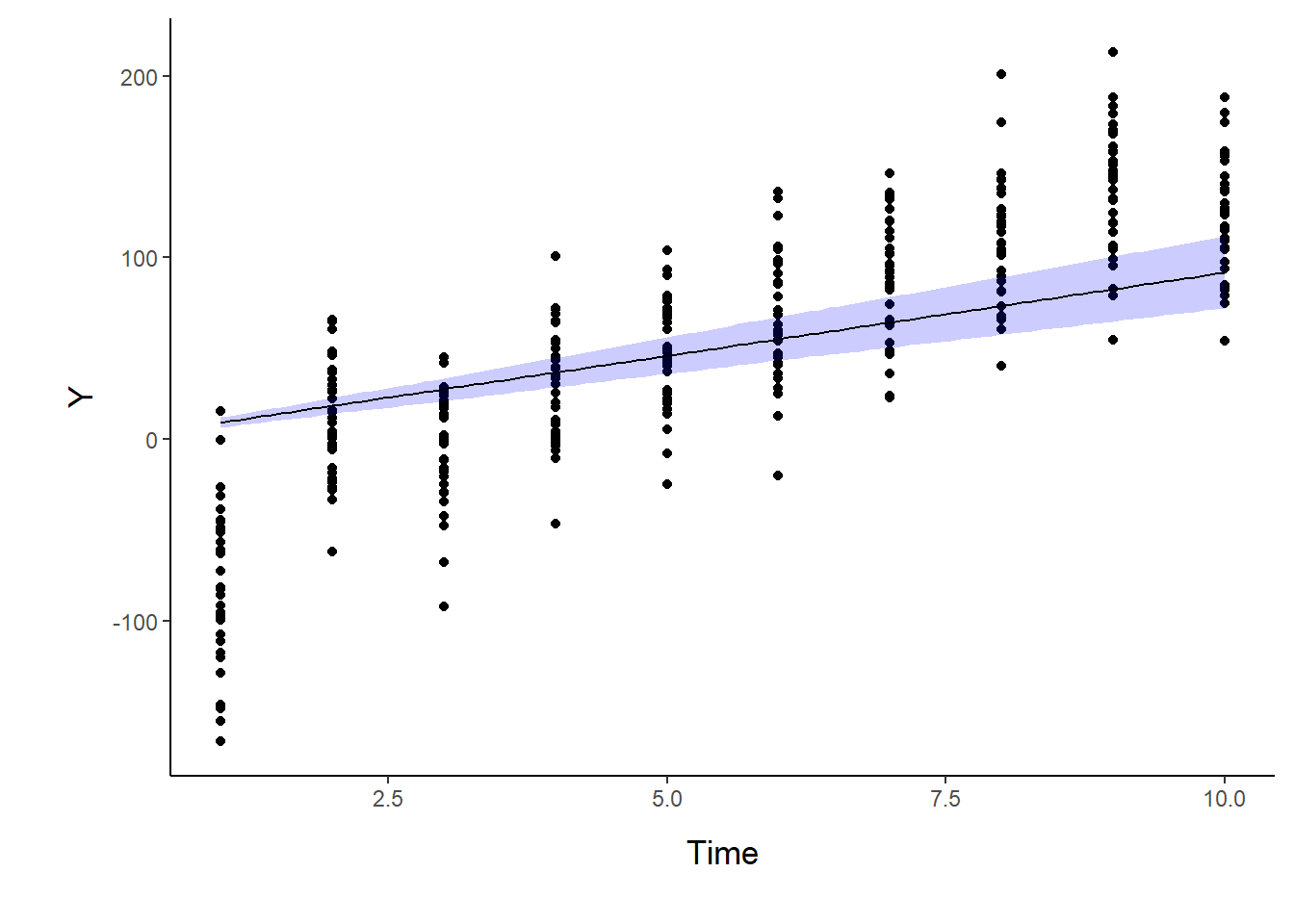
Imagine now that we has designed an experiment to investigate the effects of a continuous predictor (\(x\), for example time) on a response (\(y\)). Again, the system that we intend to sample is spatially heterogeneous and thus will add a great deal of noise to the data that will make it difficult to detect a signal (impact of treatment). Thus in an attempt to constrain this variability, we again decide to apply a design (RCB) in which each of the levels of \(X\) (such as time) treatments within each of \(35\) blocks dispersed randomly throughout the landscape. As this section is mainly about the generation of artificial data (and not specifically about what to do with the data), understanding the actual details are optional and can be safely skipped.
> set.seed(123)
> slope <- 30
> intercept <- 200
> nBlock <- 35
> nTime <- 10
> sigma <- 50
> sigma.block <- 30
> n <- nBlock*nTime
> Block <- gl(nBlock, k=1)
> Time <- 1:10
> rho <- 0.8
> dt <- expand.grid(Time=Time,Block=Block)
> Xmat <- model.matrix(~-1+Block + Time, data=dt)
> block.effects <- rnorm(n = nBlock, mean = intercept, sd = sigma.block)
> #A.effects <- c(30,40)
> all.effects <- c(block.effects,slope)
> lin.pred <- Xmat %*% all.effects
>
> # OR
> Xmat <- cbind(model.matrix(~-1+Block,data=dt),model.matrix(~Time,data=dt))
> ## Sum to zero block effects
> ##block.effects <- rnorm(n = nBlock, mean = 0, sd = sigma.block)
> ###A.effects <- c(40,70,80)
> ##all.effects <- c(block.effects,intercept,slope)
> ##lin.pred <- Xmat %*% all.effects
>
> ## the quadrat observations (within sites) are drawn from
> ## normal distributions with means according to the site means
> ## and standard deviations of 5
> eps <- NULL
> eps[1] <- 0
> for (j in 2:n) {
+ eps[j] <- rho*eps[j-1] #residuals
+ }
> y <- rnorm(n,lin.pred,sigma)+eps
>
> #OR
> eps <- NULL
> # first value cant be autocorrelated
> eps[1] <- rnorm(1,0,sigma)
> for (j in 2:n) {
+ eps[j] <- rho*eps[j-1] + rnorm(1, mean = 0, sd = sigma) #residuals
+ }
> y <- lin.pred + eps
> data.rm <- data.frame(y=y, dt)
> head(data.rm) #print out the first six rows of the data set
y Time Block
1 282.1142 1 1
2 321.1404 2 1
3 278.7700 3 1
4 285.8709 4 1
5 336.6390 5 1
6 333.5961 6 1
>
> ggplot(data.rm, aes(y=y, x=Time)) + geom_smooth(method='lm') + geom_point() + facet_wrap(~Block)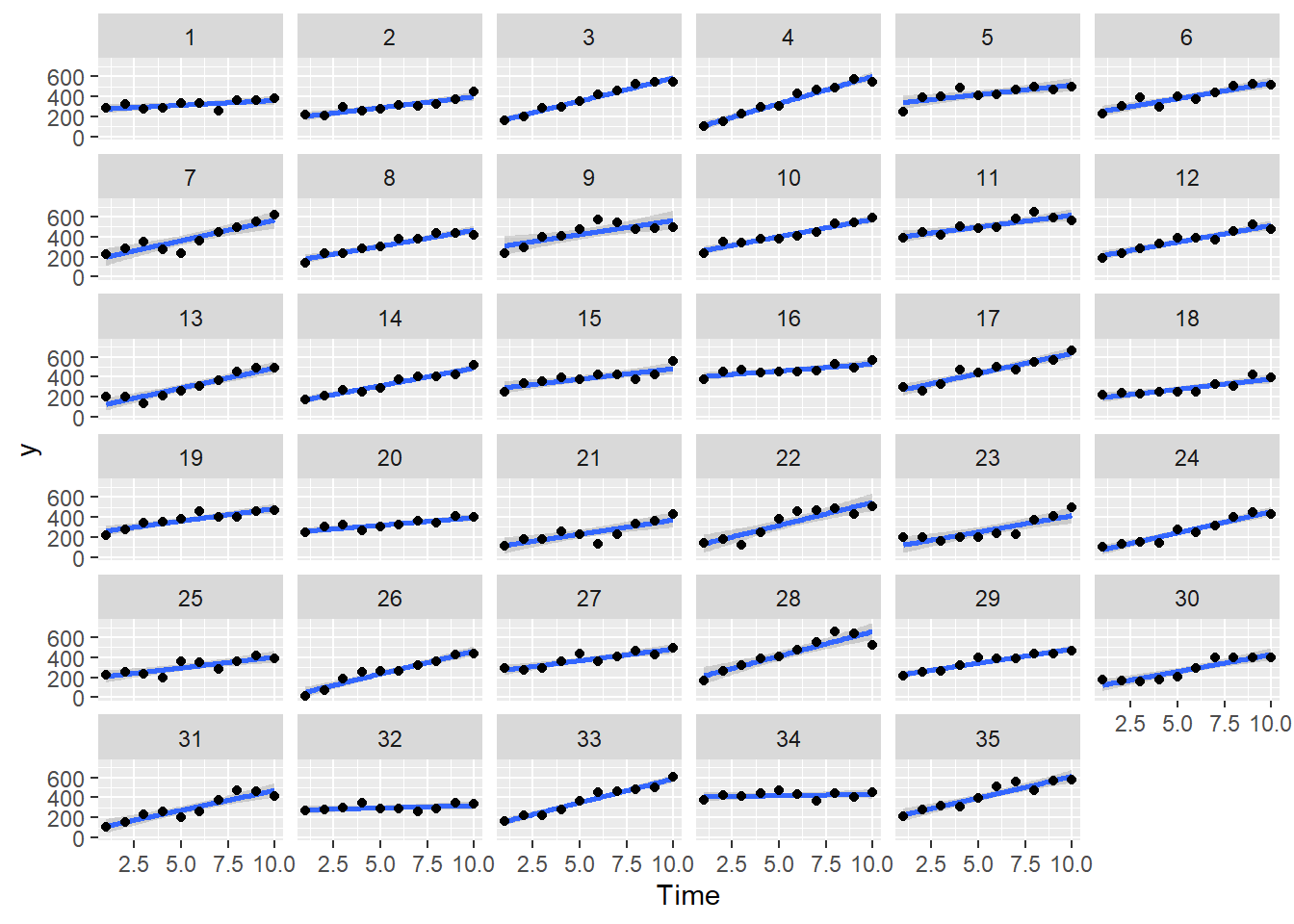
Exploratory data analysis
Normality and Homogeneity of variance
> boxplot(y~Time, data.rm)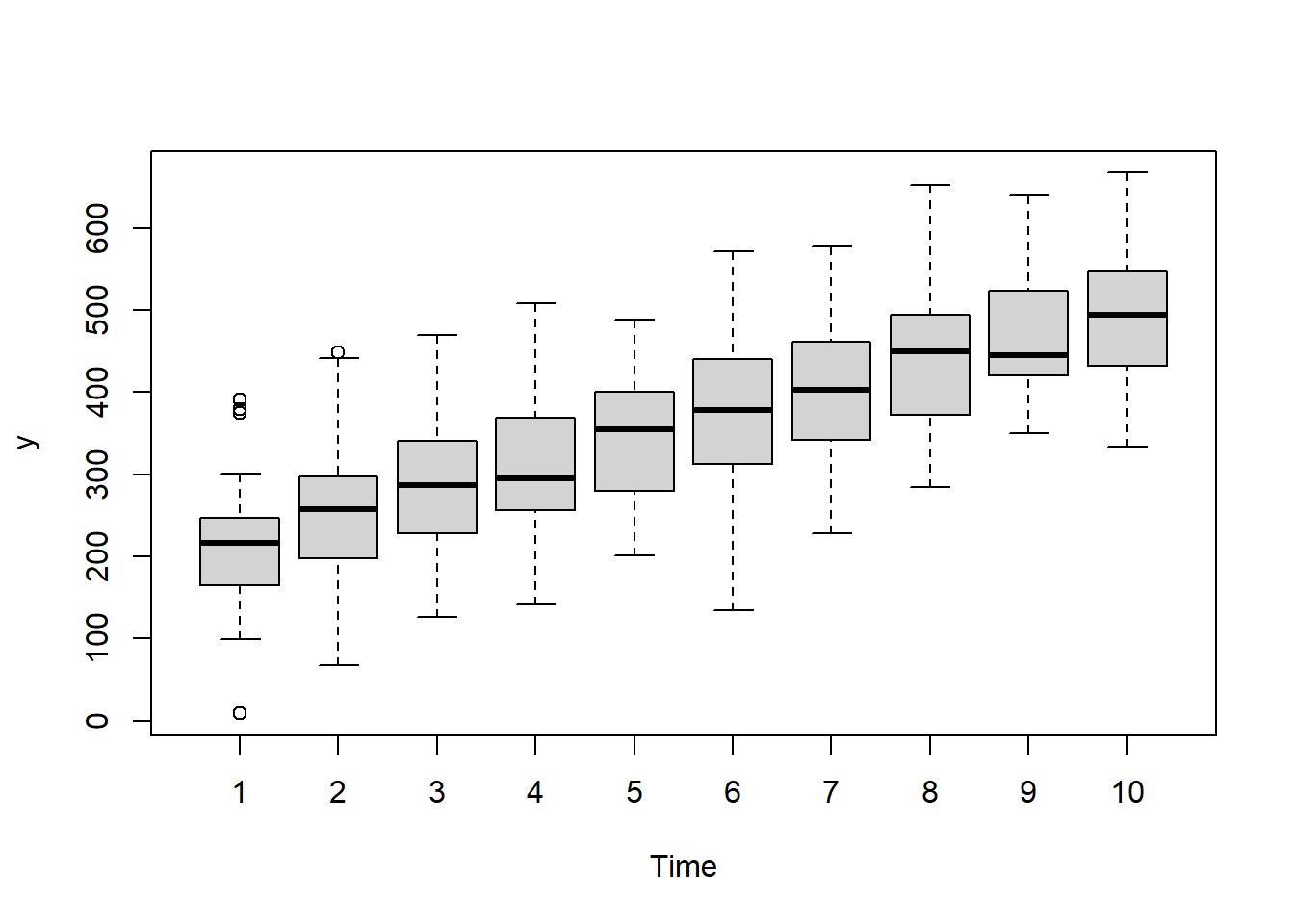
>
> ggplot(data.rm, aes(y=y, x=factor(Time))) + geom_boxplot()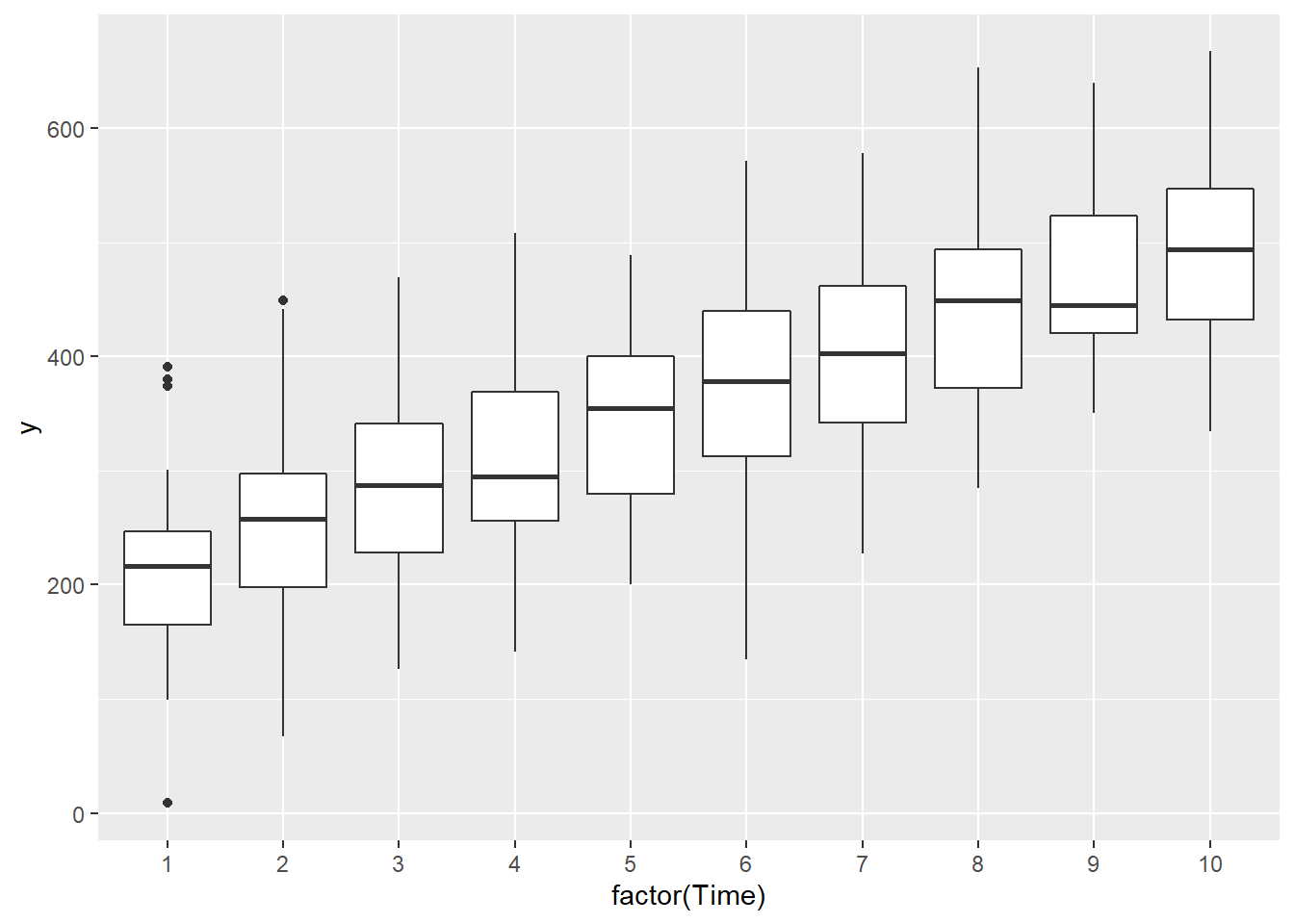
Conclusions:
there is no evidence that the response variable is consistently non-normal across all populations - each boxplot is approximately symmetrical.
there is no evidence that variance (as estimated by the height of the boxplots) differs between the five populations. More importantly, there is no evidence of a relationship between mean and variance - the height of boxplots does not increase with increasing position along the \(y\)-axis. Hence it there is no evidence of non-homogeneity
Obvious violations could be addressed either by:
- transform the scale of the response variables (to address normality, etc). Note transformations should be applied to the entire response variable (not just those populations that are skewed).
Block by within-Block interaction
> with(data.rm, interaction.plot(Time,Block,y))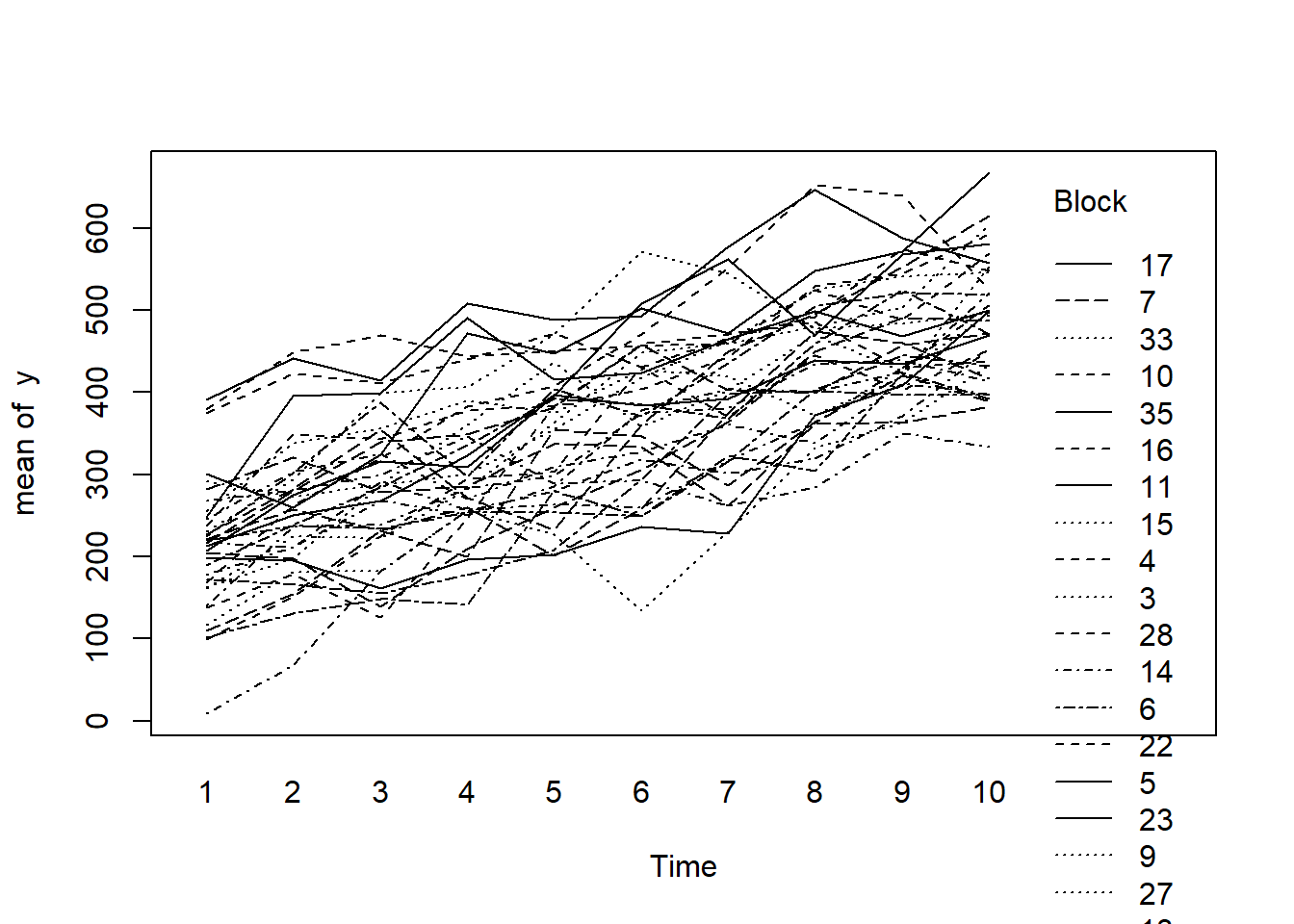
>
> ggplot(data.rm, aes(y=y, x=Time, color=Block, group=Block)) + geom_line() +
+ guides(color=guide_legend(ncol=3))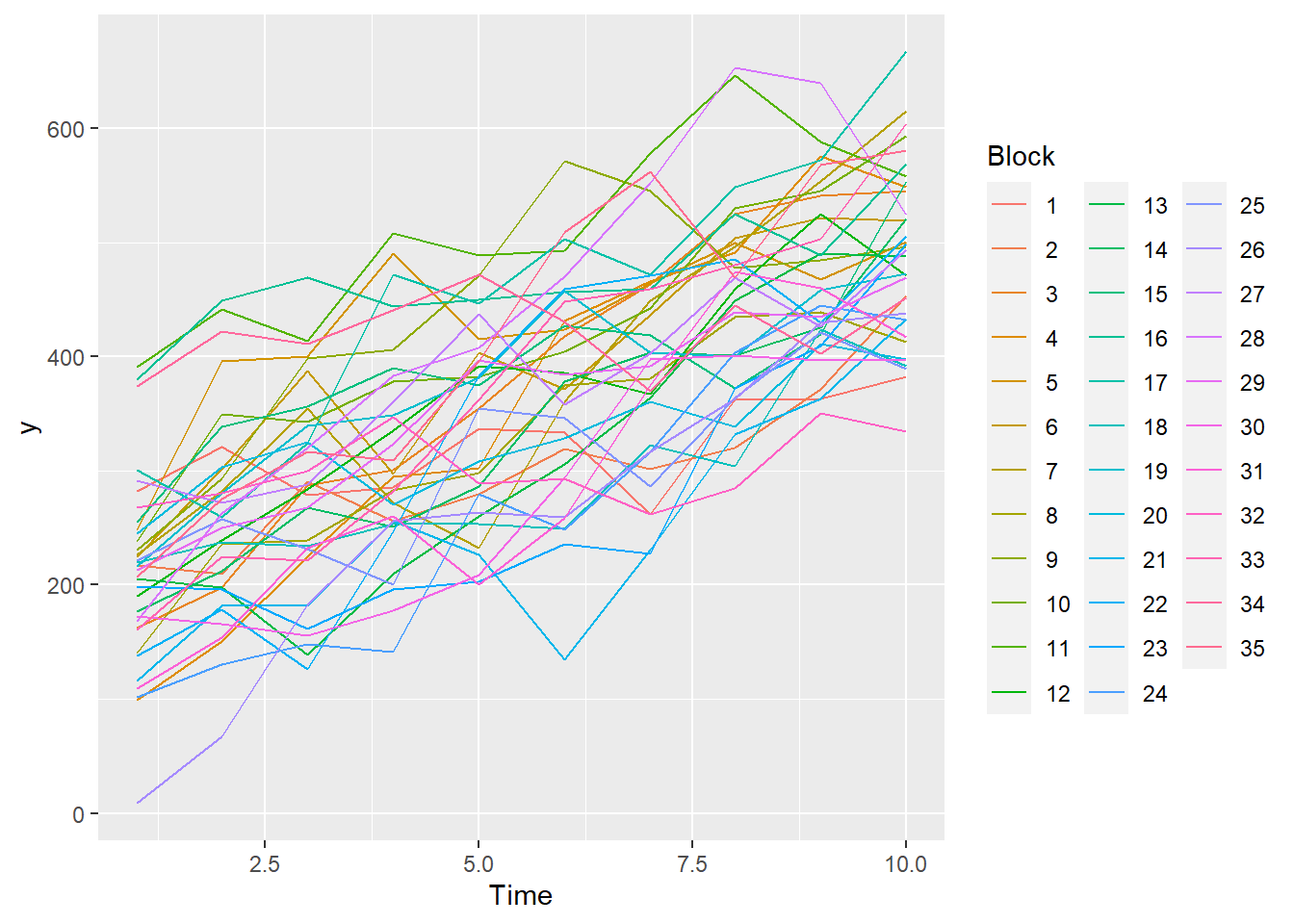
>
> residualPlots(lm(y~Block+Time, data.rm))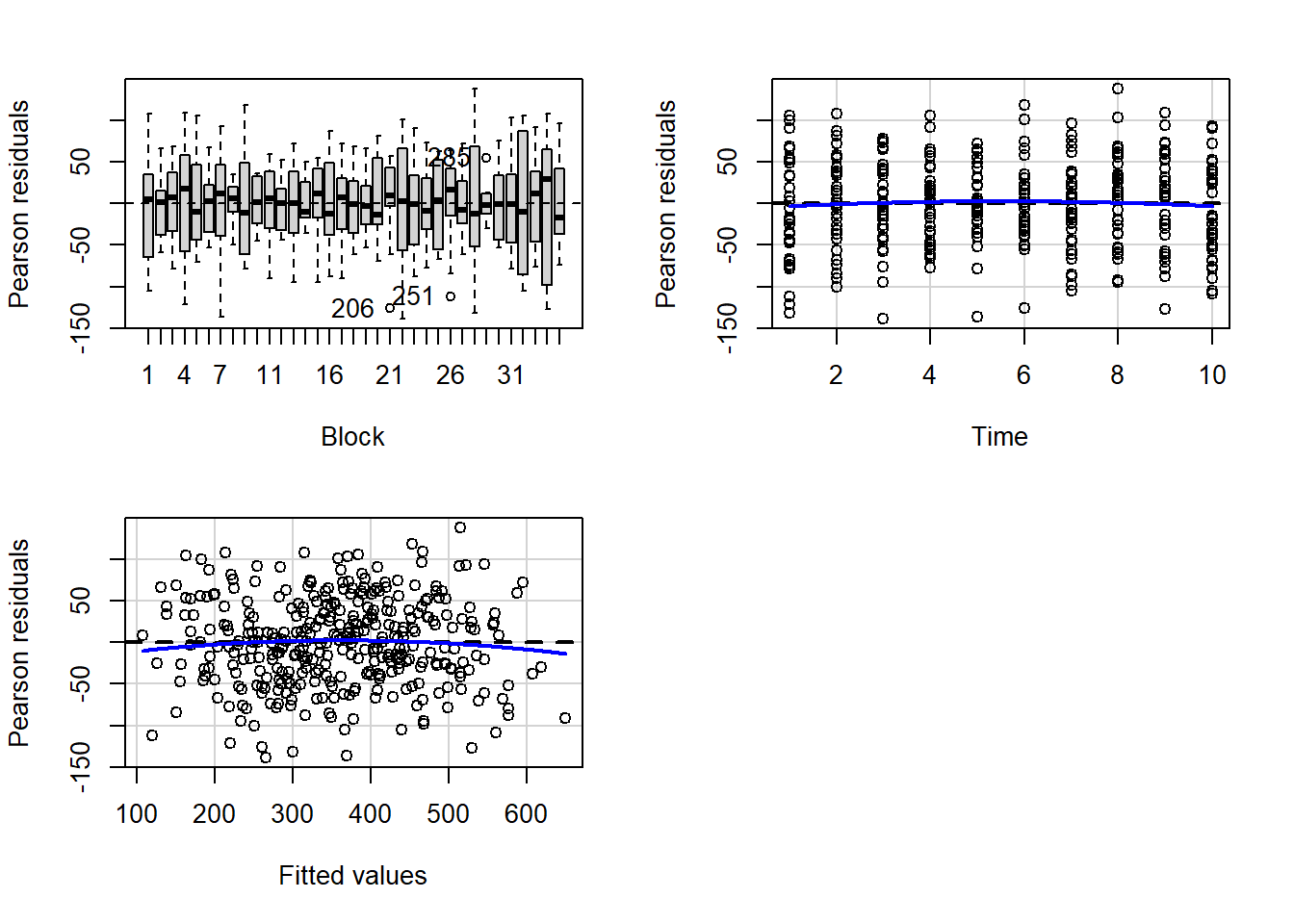
Test stat Pr(>|Test stat|)
Block
Time -0.7274 0.4675
Tukey test -0.9809 0.3267
>
> # the Tukey's non-additivity test by itself can be obtained via an internal function
> # within the car package
> car:::tukeyNonaddTest(lm(y~Block+Time, data.rm))
Test Pvalue
-0.9808606 0.3266615
>
> # alternatively, there is also a Tukey's non-additivity test within the
> # asbio package
> with(data.rm,tukey.add.test(y,Time,Block))
Tukey's one df test for additivity
F = 0.3997341 Denom df = 305 p-value = 0.5277003Conclusions:
- there is no visual or inferential evidence of any major interactions between Block and the within-Block effect (Time). Any trends appear to be reasonably consistent between Blocks.
Sphericity
Since the levels of Time cannot be randomly assigned, it is likely that sphericity is not met. We can explore whether there is an auto-correlation patterns in the residuals. Note, as there was only ten time periods, it does not make logical sense to explore lags above \(10\).
> library(nlme)
> data.rm.lme <- lme(y~Time, random=~1|Block, data=data.rm)
> acf(resid(data.rm.lme), lag=10)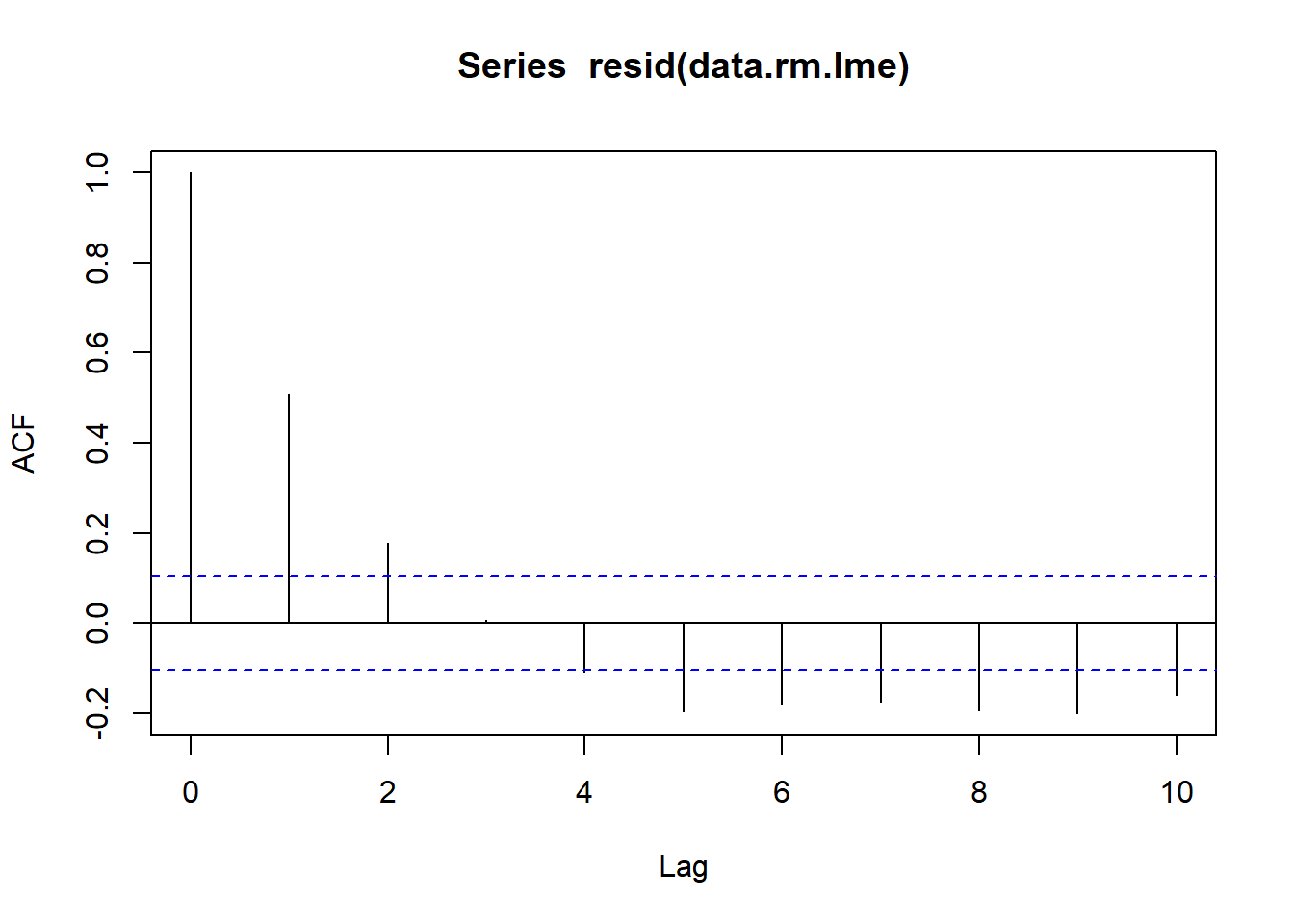
Conclusions:
The autocorrelation factor (ACF) at a range of lags up to \(10\), indicate that there is a cyclical pattern of residual auto-correlation. We really should explore incorporating some form of correlation structure into our model.
Model fitting
Full effect parameterisation
> modelString="
+ model {
+ #Likelihood
+ for (i in 1:n) {
+ y[i]~dnorm(mu[i],tau)
+ mu[i] <- beta0 + beta*Time[i] + gamma[Block[i]]
+ res[i] <- y[i]-mu[i]
+ }
+
+ #Priors
+ beta0 ~ dnorm(0, 1.0E-6)
+ beta ~ dnorm(0, 1.0E-6) #prior
+
+ for (i in 1:nBlock) {
+ gamma[i] ~ dnorm(0, tau.B) #prior
+ }
+ tau <- pow(sigma,-2)
+ sigma <- z/sqrt(chSq)
+ z ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq ~ dgamma(0.5, 0.5)
+
+ tau.B <- pow(sigma.B,-2)
+ sigma.B <- z/sqrt(chSq.B)
+ z.B ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq.B ~ dgamma(0.5, 0.5)
+ }
+ "
>
> ## write the model to a text file
> writeLines(modelString, con = "fullModel2.txt")
>
> data.rm.list <- with(data.rm,
+ list(y=y,
+ Block=as.numeric(Block),
+ Time=Time,
+ n=nrow(data.rm),
+ nBlock=length(levels(Block))
+ )
+ )
>
> params <- c("beta0","beta",'gamma',"sigma","sigma.B","res")
> burnInSteps = 3000
> nChains = 2
> numSavedSteps = 3000
> thinSteps = 1
> nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains)
>
> data.rm.r2jags.f <- jags(data = data.rm.list, inits = NULL, parameters.to.save = params,
+ model.file = "fullModel2.txt", n.chains = nChains, n.iter = nIter,
+ n.burnin = burnInSteps, n.thin = thinSteps)
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 350
Unobserved stochastic nodes: 41
Total graph size: 1815
Initializing model
>
> print(data.rm.r2jags.f)
Inference for Bugs model at "fullModel2.txt", fit using jags,
2 chains, each with 4500 iterations (first 3000 discarded)
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat
beta 30.689 1.047 28.609 30.017 30.687 31.401 32.705 1.001
beta0 189.009 12.648 164.589 180.318 189.054 197.523 213.976 1.001
gamma[1] -35.015 20.219 -74.991 -47.706 -35.021 -21.382 3.826 1.002
gamma[2] -52.026 20.114 -91.663 -65.012 -52.008 -38.575 -12.685 1.001
gamma[3] 20.417 19.878 -19.313 7.462 20.587 33.579 60.228 1.001
gamma[4] 0.671 20.295 -38.799 -12.839 0.882 14.490 39.807 1.001
gamma[5] 67.812 19.967 29.683 54.189 67.514 81.150 109.392 1.001
gamma[6] 36.338 19.760 -2.575 22.780 36.203 49.381 76.772 1.001
gamma[7] 24.072 20.155 -14.701 10.740 24.009 36.728 63.397 1.001
gamma[8] -31.199 20.016 -70.564 -44.687 -31.149 -17.691 7.011 1.001
gamma[9] 73.971 20.034 35.053 60.309 73.846 87.726 113.132 1.003
gamma[10] 58.034 19.900 19.397 44.730 58.085 71.380 97.283 1.001
gamma[11] 141.644 20.387 101.956 127.950 141.240 154.897 181.751 1.001
gamma[12] 5.655 20.094 -32.833 -7.787 5.349 19.065 47.017 1.001
gamma[13] -44.187 20.168 -84.778 -57.576 -44.641 -30.571 -5.599 1.001
gamma[14] -23.866 19.908 -63.673 -37.311 -23.653 -10.578 14.435 1.001
gamma[15] 30.407 20.239 -8.109 16.928 30.379 43.830 70.587 1.001
gamma[16] 103.433 20.123 64.608 90.052 103.087 116.736 143.495 1.002
gamma[17] 91.556 20.060 53.115 77.561 91.725 104.473 131.814 1.002
gamma[18] -63.563 20.127 -102.913 -77.195 -63.210 -50.190 -24.916 1.002
gamma[19] 16.404 19.820 -21.892 2.880 16.232 29.420 55.497 1.001
gamma[20] -26.858 19.837 -66.283 -39.890 -26.676 -13.651 12.760 1.002
gamma[21] -104.771 19.743 -143.174 -117.701 -105.347 -92.448 -64.620 1.001
gamma[22] -14.307 19.903 -54.617 -27.704 -14.041 -0.901 23.918 1.001
gamma[23] -81.493 19.863 -121.932 -94.860 -81.367 -67.618 -43.350 1.001
gamma[24] -86.520 20.067 -125.826 -100.133 -86.297 -73.003 -47.481 1.001
gamma[25] -47.166 20.417 -86.549 -61.568 -47.155 -33.479 -6.020 1.001
gamma[26] -92.375 19.497 -130.380 -105.540 -92.310 -79.043 -54.017 1.002
gamma[27] 20.875 20.031 -18.328 6.625 20.873 34.275 60.661 1.002
gamma[28] 74.464 19.909 36.179 61.091 74.369 87.433 114.480 1.001
gamma[29] -0.792 19.771 -39.202 -14.402 -0.589 12.677 36.999 1.001
gamma[30] -75.855 20.350 -116.077 -89.286 -76.179 -62.465 -35.911 1.001
gamma[31] -58.457 20.104 -97.479 -72.394 -58.390 -44.695 -19.492 1.001
gamma[32] -53.274 20.080 -91.482 -66.984 -53.201 -40.309 -13.057 1.001
gamma[33] 15.405 20.131 -22.770 1.695 15.048 28.831 55.869 1.001
gamma[34] 59.338 20.334 19.750 45.810 59.517 72.790 99.194 1.001
gamma[35] 56.933 20.301 15.197 43.906 57.388 70.588 94.583 1.001
res[1] 97.432 17.921 62.629 85.359 97.337 109.111 134.580 1.002
res[2] 105.769 17.698 71.182 93.805 105.826 117.408 142.144 1.002
res[3] 32.710 17.534 -1.148 20.909 32.522 44.178 68.460 1.002
res[4] 9.121 17.431 -23.865 -2.637 8.871 20.532 44.239 1.002
res[5] 29.201 17.391 -4.021 17.641 28.835 40.540 64.071 1.002
res[6] -4.531 17.414 -38.094 -16.092 -4.863 6.832 30.205 1.002
res[7] -107.185 17.500 -140.651 -118.950 -107.516 -95.741 -72.125 1.002
res[8] -37.350 17.647 -71.015 -49.217 -37.556 -25.708 -1.746 1.002
res[9] -67.307 17.855 -101.635 -79.246 -67.326 -55.699 -31.035 1.002
res[10] -78.614 18.121 -113.985 -90.735 -78.654 -66.764 -42.063 1.002
res[11] 49.884 18.193 13.728 37.834 50.102 61.789 84.845 1.001
res[12] 11.595 17.930 -23.183 -0.446 11.692 23.269 46.321 1.001
res[13] 61.820 17.726 27.566 49.860 61.924 73.375 96.299 1.001
res[14] -3.458 17.582 -37.401 -15.192 -3.465 8.046 30.969 1.001
res[15] -10.511 17.499 -44.587 -21.767 -10.459 1.089 24.112 1.001
res[16] -2.243 17.479 -36.572 -13.604 -2.049 9.337 32.255 1.001
res[17] -50.520 17.522 -85.179 -61.867 -50.373 -38.782 -16.278 1.001
res[18] -62.585 17.627 -97.953 -73.969 -62.501 -50.564 -28.305 1.001
res[19] -42.079 17.792 -77.762 -53.482 -42.166 -30.142 -7.621 1.001
res[20] 9.165 18.018 -26.988 -2.455 9.147 21.271 43.778 1.001
res[21] -77.926 17.501 -113.047 -89.469 -78.006 -66.052 -43.688 1.002
res[22] -73.189 17.257 -108.057 -84.536 -73.411 -61.442 -39.850 1.002
res[23] -14.228 17.075 -48.379 -25.553 -14.413 -2.773 18.665 1.002
res[24] -31.958 16.955 -66.594 -43.263 -32.141 -20.655 0.554 1.002
res[25] -7.975 16.900 -42.439 -19.028 -8.192 3.408 24.762 1.002
res[26] 24.320 16.909 -9.262 13.308 24.202 35.576 57.313 1.002
res[27] 38.799 16.983 5.216 27.563 38.571 50.247 72.421 1.002
res[28] 69.516 17.120 35.582 58.330 69.291 80.872 103.259 1.002
res[29] 55.153 17.321 20.895 43.887 54.848 66.615 89.335 1.002
res[30] 28.976 17.581 -5.726 17.342 28.565 40.577 63.635 1.002
res[31] -121.587 17.872 -156.152 -133.567 -121.526 -109.634 -87.382 1.001
res[32] -100.256 17.618 -133.884 -111.966 -100.063 -88.659 -66.409 1.001
res[33] -57.168 17.423 -90.542 -68.902 -57.110 -45.627 -22.964 1.001
res[34] -17.580 17.290 -51.232 -29.462 -17.603 -6.075 16.449 1.001
res[35] -40.581 17.219 -74.430 -52.498 -40.599 -29.045 -6.738 1.001
res[36] 57.619 17.212 23.794 45.812 57.457 69.114 91.210 1.001
res[37] 61.388 17.269 27.008 49.782 61.277 72.884 95.367 1.004
res[38] 56.259 17.389 21.473 44.753 56.294 67.702 90.416 1.001
res[39] 109.316 17.570 73.992 97.577 109.390 120.643 143.528 1.001
res[40] 52.088 17.811 16.206 39.944 52.135 63.655 86.709 1.001
res[41] -38.914 17.643 -73.656 -50.658 -38.634 -26.860 -5.046 1.001
res[42] 77.326 17.420 42.616 65.720 77.575 89.215 111.120 1.001
res[43] 50.865 17.258 16.915 39.497 51.222 62.617 84.564 1.001
res[44] 110.679 17.159 76.469 99.239 111.186 122.203 144.204 1.001
res[45] 4.790 17.122 -29.711 -6.616 5.343 16.301 38.330 1.001
res[46] -17.661 17.150 -52.491 -29.227 -17.113 -5.957 16.017 1.001
res[47] -7.311 17.242 -42.494 -18.933 -6.757 4.462 26.166 1.001
res[48] -3.089 17.396 -38.865 -14.616 -2.473 8.846 31.113 1.001
res[49] -65.133 17.611 -101.697 -76.777 -64.519 -53.174 -30.398 1.001
res[50] -63.661 17.886 -100.707 -75.693 -63.048 -51.501 -28.264 1.001
res[51] -31.518 17.144 -65.465 -43.209 -31.355 -19.712 1.672 1.001
res[52] 14.815 16.893 -18.897 3.470 14.776 26.305 47.890 1.001
res[53] 70.347 16.704 36.921 58.939 70.092 81.766 102.877 1.001
res[54] -50.853 16.579 -83.834 -62.055 -51.073 -39.619 -18.942 1.001
res[55] 25.083 16.520 -8.057 14.027 24.935 36.357 56.754 1.001
res[56] -38.143 16.527 -71.222 -49.423 -38.357 -26.836 -6.450 1.001
res[57] -4.070 16.600 -36.763 -15.317 -4.236 7.197 27.724 1.001
res[58] 33.306 16.738 0.513 22.191 33.191 44.522 65.598 1.001
res[59] 20.080 16.940 -12.937 8.828 19.836 31.550 52.764 1.001
res[60] -12.900 17.204 -46.161 -24.276 -13.088 -1.463 20.472 1.001
res[61] -17.368 17.885 -51.348 -29.241 -17.425 -5.291 18.072 1.001
res[62] 7.369 17.652 -26.193 -4.253 7.234 19.236 42.448 1.001
res[63] 49.245 17.479 15.639 37.647 49.046 60.880 83.698 1.001
res[64] -64.174 17.368 -97.742 -75.711 -64.357 -52.534 -30.120 1.001
res[65] -134.249 17.320 -167.266 -146.107 -134.437 -122.586 -100.604 1.001
res[66] -37.107 17.334 -70.680 -48.991 -37.270 -25.543 -3.298 1.001
res[67] 21.279 17.412 -12.492 9.532 21.267 33.096 55.105 1.001
res[68] 37.284 17.552 3.245 25.564 37.265 49.184 71.420 1.001
res[69] 63.944 17.753 29.095 52.068 63.864 75.938 98.781 1.001
res[70] 95.234 18.013 60.203 83.123 95.270 107.455 130.632 1.001
res[71] -48.396 17.620 -83.102 -60.471 -48.230 -36.426 -13.894 1.001
res[72] 16.818 17.403 -17.131 4.932 16.936 28.621 50.566 1.001
res[73] -10.912 17.247 -44.871 -22.609 -10.795 0.606 22.307 1.001
res[74] 2.547 17.154 -31.372 -8.982 2.664 14.012 35.509 1.001
res[75] -13.113 17.125 -47.212 -24.603 -12.951 -1.578 20.054 1.001
res[76] 32.577 17.159 -1.807 20.989 32.596 44.219 65.805 1.001
res[77] 7.970 17.257 -27.008 -3.791 7.911 19.682 41.186 1.001
res[78] 31.495 17.418 -3.602 19.914 31.400 43.395 65.506 1.001
res[79] 4.718 17.639 -30.550 -6.860 4.806 16.702 39.109 1.001
res[80] -51.946 17.919 -87.119 -63.726 -51.922 -39.897 -17.025 1.001
res[81] -63.210 17.647 -97.791 -75.690 -63.212 -51.190 -29.440 1.002
res[82] -31.067 17.390 -65.386 -43.236 -31.079 -19.273 2.374 1.002
res[83] 43.678 17.193 9.558 31.772 43.540 55.495 76.981 1.002
res[84] 20.380 17.058 -13.497 8.805 20.360 32.176 53.934 1.002
res[85] 54.597 16.986 21.096 43.276 54.749 66.249 87.971 1.002
res[86] 124.353 16.979 90.938 113.063 124.583 135.902 157.927 1.002
res[87] 67.176 17.037 33.903 55.809 67.439 78.691 101.104 1.002
res[88] -30.778 17.158 -64.046 -42.370 -30.407 -19.292 2.913 1.002
res[89] -55.098 17.342 -88.751 -66.851 -54.716 -43.392 -21.208 1.002
res[90] -73.427 17.586 -107.590 -85.203 -73.116 -61.615 -38.693 1.002
res[91] -39.879 17.759 -75.389 -51.772 -39.985 -28.068 -4.896 1.001
res[92] 40.803 17.486 5.829 29.249 40.623 52.320 75.462 1.001
res[93] 3.288 17.272 -30.880 -8.346 3.017 14.813 37.091 1.001
res[94] 8.096 17.120 -26.071 -3.487 7.840 19.496 41.421 1.001
res[95] -18.230 17.031 -51.683 -29.609 -18.372 -6.678 14.819 1.001
res[96] -27.022 17.006 -60.187 -38.426 -27.134 -15.863 6.296 1.001
res[97] -19.513 17.045 -52.825 -30.880 -19.632 -8.423 13.668 1.001
res[98] 37.064 17.149 3.831 25.570 37.124 48.265 70.659 1.001
res[99] 21.843 17.315 -12.203 10.180 21.878 33.093 55.675 1.001
res[100] 39.105 17.542 5.025 27.487 38.948 50.788 73.056 1.001
res[101] 29.449 17.991 -5.205 17.155 29.781 41.807 63.442 1.001
res[102] 49.685 17.766 15.218 37.673 50.072 61.814 82.819 1.001
res[103] -8.723 17.601 -43.029 -20.739 -8.303 3.244 24.590 1.001
res[104] 54.477 17.498 20.833 42.653 54.759 66.407 87.773 1.001
res[105] 4.508 17.456 -29.390 -7.159 4.817 16.421 37.676 1.001
res[106] -21.847 17.477 -55.720 -33.395 -21.535 -9.860 11.772 1.001
res[107] 32.423 17.561 -2.084 20.791 32.811 44.448 66.578 1.001
res[108] 70.203 17.706 35.619 58.406 70.311 82.156 104.571 1.001
res[109] -18.915 17.912 -54.616 -30.740 -18.911 -6.868 15.481 1.001
res[110] -79.501 18.176 -115.834 -91.501 -79.578 -67.080 -44.590 1.001
res[111] -35.407 17.785 -70.692 -46.976 -35.584 -23.160 -0.930 1.001
res[112] -16.834 17.533 -51.394 -28.356 -17.011 -4.647 17.012 1.001
res[113] -2.964 17.342 -37.311 -14.283 -3.253 9.068 30.829 1.001
res[114] 17.958 17.211 -16.244 6.888 17.697 29.740 51.566 1.001
res[115] 43.960 17.144 9.743 32.909 43.779 55.749 77.773 1.002
res[116] 6.922 17.141 -27.302 -4.089 6.746 18.522 41.245 1.002
res[117] -42.437 17.202 -76.634 -53.389 -42.592 -31.097 -7.471 1.002
res[118] 18.962 17.325 -15.305 7.723 18.882 30.432 53.655 1.003
res[119] 54.157 17.511 19.505 42.669 54.007 65.841 88.924 1.003
res[120] -30.836 17.757 -66.091 -42.472 -31.031 -18.943 4.597 1.003
res[121] 29.694 17.913 -5.583 17.603 29.789 41.163 65.302 1.001
res[122] -8.428 17.668 -42.894 -20.446 -8.260 2.790 26.838 1.001
res[123] -97.805 17.483 -132.040 -109.658 -97.722 -86.688 -63.003 1.001
res[124] -58.400 17.360 -92.551 -70.268 -58.013 -47.184 -24.118 1.001
res[125] -38.480 17.298 -72.858 -50.159 -38.072 -27.272 -4.162 1.001
res[126] -23.590 17.301 -58.378 -35.298 -23.103 -12.266 10.906 1.001
res[127] 3.860 17.366 -31.068 -7.655 4.299 15.220 38.206 1.001
res[128] 58.998 17.494 23.758 47.395 59.472 70.391 93.062 1.001
res[129] 69.127 17.683 33.354 57.321 69.673 80.505 103.147 1.001
res[130] 35.991 17.931 -0.747 24.279 36.423 47.825 70.397 1.001
res[131] -18.707 17.753 -53.599 -30.549 -18.607 -6.714 16.819 1.003
res[132] -14.747 17.516 -48.954 -26.537 -14.555 -2.845 20.061 1.003
res[133] 10.374 17.340 -23.749 -1.370 10.597 22.133 44.664 1.003
res[134] -37.152 17.225 -70.611 -48.839 -37.026 -25.712 -3.136 1.002
res[135] -32.541 17.174 -65.860 -44.108 -32.536 -21.077 1.265 1.002
res[136] 28.588 17.186 -4.848 17.066 28.625 39.992 62.044 1.002
res[137] 23.576 17.262 -10.078 11.987 23.698 35.092 57.117 1.002
res[138] -10.078 17.401 -43.670 -21.709 -9.920 1.610 23.933 1.001
res[139] -16.016 17.601 -49.961 -27.799 -15.770 -4.358 18.774 1.001
res[140] 48.626 17.861 14.303 36.410 48.905 60.610 83.764 1.001
res[141] 4.593 17.780 -29.625 -7.191 4.424 16.505 38.788 1.001
res[142] 57.463 17.544 23.749 45.968 57.368 69.300 91.358 1.001
res[143] 44.743 17.368 11.543 33.225 44.780 56.414 78.495 1.001
res[144] 47.987 17.253 14.659 36.564 48.140 59.625 81.776 1.001
res[145] 2.009 17.202 -31.053 -9.596 2.094 13.679 35.963 1.001
res[146] 23.279 17.214 -9.893 11.605 23.253 34.820 57.175 1.001
res[147] -15.427 17.290 -49.433 -27.118 -15.449 -4.007 19.070 1.001
res[148] -92.242 17.428 -126.419 -104.123 -92.223 -80.822 -57.405 1.001
res[149] -76.403 17.628 -110.319 -88.293 -76.440 -64.957 -41.280 1.001
res[150] 27.022 17.887 -7.788 14.991 26.934 38.901 62.553 1.001
res[151] 56.524 17.435 23.497 44.650 56.376 68.008 91.937 1.002
res[152] 94.888 17.193 62.473 83.265 94.748 106.107 129.551 1.001
res[153] 85.122 17.012 53.069 73.707 84.983 96.084 119.032 1.001
res[154] 28.800 16.893 -3.079 17.754 28.668 39.844 62.380 1.001
res[155] 3.921 16.839 -28.102 -7.248 3.904 15.053 37.301 1.001
res[156] -19.671 16.850 -51.711 -30.814 -19.649 -8.511 13.270 1.001
res[157] -48.454 16.926 -81.115 -59.563 -48.405 -37.301 -15.678 1.001
res[158] -12.976 17.067 -46.088 -24.257 -12.925 -1.706 20.012 1.001
res[159] -79.807 17.269 -113.216 -91.035 -79.682 -68.569 -46.865 1.001
res[160] -30.224 17.532 -64.395 -41.789 -29.847 -18.816 2.893 1.001
res[161] -10.710 17.984 -46.042 -22.979 -10.276 1.572 24.298 1.002
res[162] -82.452 17.740 -118.119 -94.601 -82.059 -70.317 -47.916 1.002
res[163] -48.077 17.555 -83.627 -59.974 -47.795 -35.994 -13.951 1.002
res[164] 68.821 17.431 33.752 56.976 68.995 80.691 102.233 1.005
res[165] 12.830 17.369 -22.123 1.019 12.897 24.719 45.628 1.002
res[166] 38.006 17.370 3.280 26.085 37.983 49.937 71.003 1.002
res[167] -23.347 17.435 -58.240 -35.377 -23.237 -11.414 9.865 1.002
res[168] 22.078 17.561 -13.256 9.887 22.185 34.157 55.218 1.001
res[169] 15.237 17.749 -20.525 3.105 15.325 27.296 48.552 1.001
res[170] 79.730 17.996 43.542 67.295 79.674 91.820 113.635 1.002
res[171] 63.717 17.877 28.767 51.218 63.625 75.992 98.346 1.002
res[172] 50.693 17.611 16.356 38.398 50.624 62.696 84.475 1.001
res[173] 16.355 17.405 -17.386 4.388 16.412 28.087 49.899 1.001
res[174] 5.229 17.259 -28.246 -6.690 5.281 16.848 38.937 1.001
res[175] -25.424 17.176 -58.537 -37.419 -25.426 -13.955 7.970 1.001
res[176] -60.299 17.157 -93.240 -72.218 -60.299 -48.754 -26.651 1.001
res[177] -17.707 17.202 -50.497 -29.605 -17.777 -6.222 15.477 1.001
res[178] -67.087 17.310 -99.859 -79.145 -67.067 -55.435 -33.398 1.001
res[179] 21.851 17.480 -10.981 9.770 21.871 33.713 56.070 1.001
res[180] -40.647 17.711 -73.957 -52.771 -40.513 -28.613 -5.841 1.001
res[181] -19.458 17.542 -54.333 -31.085 -19.422 -7.722 15.640 1.001
res[182] 13.382 17.297 -20.657 2.031 13.446 24.888 47.985 1.001
res[183] 42.203 17.113 8.488 30.978 42.207 53.606 75.709 1.001
res[184] 20.699 16.991 -12.648 9.734 20.572 32.070 53.897 1.001
res[185] 22.419 16.933 -10.796 11.505 22.206 33.885 55.335 1.001
res[186] 67.746 16.941 34.410 57.004 67.445 79.392 100.423 1.001
res[187] -17.017 17.012 -50.239 -27.920 -17.298 -5.427 15.763 1.001
res[188] -51.228 17.148 -84.441 -62.328 -51.548 -39.688 -18.069 1.001
res[189] -23.628 17.345 -57.805 -34.767 -23.760 -11.997 10.684 1.001
res[190] -39.945 17.603 -74.634 -51.215 -40.154 -28.208 -5.214 1.001
res[191] 52.530 17.512 18.626 41.139 52.206 64.088 87.150 1.006
res[192] 79.593 17.246 46.248 68.448 79.388 91.100 113.049 1.017
res[193] 71.051 17.040 37.868 59.980 70.793 82.571 104.153 1.021
res[194] -14.917 16.897 -48.034 -25.902 -15.296 -3.462 18.041 1.005
res[195] -7.135 16.817 -39.943 -18.047 -7.544 4.215 25.897 1.005
res[196] -18.174 16.803 -51.133 -29.182 -18.623 -6.895 14.827 1.005
res[197] -16.439 16.854 -48.969 -27.463 -16.762 -5.147 16.557 1.004
res[198] -69.150 16.970 -102.173 -80.328 -69.361 -57.572 -35.980 1.004
res[199] -27.445 17.149 -60.854 -38.683 -27.690 -15.800 6.299 1.003
res[200] -71.100 17.389 -104.684 -82.727 -71.394 -59.189 -37.691 1.003
res[201] 1.426 17.309 -34.407 -9.571 1.332 12.962 35.011 1.001
res[202] 36.131 17.046 0.771 25.266 36.227 47.347 69.464 1.001
res[203] 5.510 16.844 -28.967 -5.374 5.685 16.535 38.753 1.001
res[204] 49.200 16.705 15.453 38.505 49.435 60.187 82.079 1.001
res[205] -10.960 16.631 -44.546 -21.713 -10.492 -0.147 21.703 1.001
res[206] -133.889 16.623 -167.539 -144.693 -133.301 -123.036 -101.431 1.001
res[207] -68.634 16.681 -102.616 -79.683 -67.975 -57.769 -36.182 1.001
res[208] 2.212 16.804 -31.897 -8.838 2.830 13.283 34.752 1.001
res[209] 2.431 16.991 -31.627 -8.767 3.000 13.550 35.269 1.001
res[210] 41.968 17.240 6.811 30.539 42.440 53.467 75.061 1.001
res[211] -67.622 17.508 -102.075 -79.236 -67.541 -56.136 -32.937 1.001
res[212] -57.530 17.266 -91.092 -68.962 -57.500 -46.025 -22.873 1.001
res[213] -140.313 17.084 -173.718 -151.700 -140.155 -128.926 -105.859 1.002
res[214] -50.542 16.964 -83.840 -61.841 -50.386 -39.139 -16.241 1.002
res[215] 55.074 16.909 22.122 43.726 55.352 66.374 89.195 1.002
res[216] 100.133 16.919 67.118 88.860 100.592 111.422 133.899 1.002
res[217] 80.975 16.993 48.141 69.704 81.338 92.108 115.080 1.002
res[218] 65.212 17.132 32.285 53.430 65.470 76.536 100.152 1.001
res[219] -21.674 17.332 -55.118 -33.640 -21.456 -10.022 13.856 1.002
res[220] 24.003 17.593 -9.530 11.811 24.101 35.907 59.852 1.002
res[221] 60.185 17.783 25.820 48.457 59.813 72.436 96.171 1.001
res[222] 26.825 17.539 -6.907 15.267 26.510 38.780 62.320 1.001
res[223] -37.765 17.355 -71.270 -49.250 -38.173 -25.946 -2.142 1.001
res[224] -33.962 17.232 -67.496 -45.390 -34.499 -22.046 1.130 1.001
res[225] -58.522 17.173 -91.829 -70.044 -59.083 -46.732 -23.657 1.001
res[226] -55.706 17.177 -88.390 -67.397 -56.263 -44.042 -21.182 1.001
res[227] -94.620 17.245 -127.457 -106.411 -95.119 -82.969 -60.749 1.001
res[228] 19.371 17.375 -13.948 7.607 19.044 31.010 53.459 1.001
res[229] 25.246 17.568 -8.529 13.626 24.828 37.075 59.410 1.001
res[230] 84.355 17.820 50.467 72.405 83.982 96.570 118.968 1.001
res[231] -31.497 18.030 -66.696 -43.447 -31.785 -19.738 3.853 1.001
res[232] -33.555 17.750 -68.255 -45.064 -33.695 -22.067 1.221 1.001
res[233] -46.454 17.529 -80.525 -58.085 -46.585 -35.121 -11.905 1.001
res[234] -84.283 17.368 -118.128 -95.729 -84.398 -73.094 -50.480 1.001
res[235] 23.792 17.270 -9.429 12.004 23.713 34.911 57.625 1.001
res[236] -37.979 17.234 -71.525 -49.693 -38.039 -26.826 -3.726 1.001
res[237] -0.851 17.262 -34.217 -12.666 -0.823 10.179 33.380 1.001
res[238] 55.116 17.354 21.132 43.276 55.278 66.313 89.932 1.001
res[239] 66.340 17.507 31.871 54.397 66.435 77.816 102.154 1.001
res[240] 22.509 17.721 -12.331 10.444 22.467 34.188 58.690 1.001
res[241] 48.779 17.985 13.144 36.603 49.101 61.358 82.744 1.001
res[242] 54.607 17.728 19.723 42.634 54.853 67.014 88.097 1.001
res[243] -2.573 17.531 -36.920 -14.310 -2.250 9.522 31.153 1.001
res[244] -64.682 17.394 -98.704 -76.398 -64.353 -52.693 -31.136 1.001
res[245] 59.232 17.320 25.143 47.518 59.597 70.983 92.873 1.001
res[246] 19.963 17.309 -14.316 8.145 20.310 31.886 53.371 1.001
res[247] -70.443 17.361 -105.373 -82.320 -70.049 -58.397 -36.717 1.001
res[248] -23.463 17.476 -58.679 -35.360 -23.248 -11.587 10.598 1.001
res[249] 2.831 17.652 -32.482 -8.951 3.087 14.786 37.287 1.001
res[250] -59.475 17.888 -95.014 -71.176 -59.315 -47.543 -24.802 1.001
res[251] -118.664 17.326 -151.645 -130.208 -118.894 -107.309 -83.446 1.002
res[252] -91.020 17.066 -123.512 -102.427 -91.199 -79.836 -57.008 1.001
res[253] -6.258 16.868 -38.555 -17.830 -6.464 4.709 27.751 1.001
res[254] 36.251 16.734 4.248 24.639 35.981 47.226 70.217 1.001
res[255] 13.667 16.664 -18.023 2.118 13.400 24.523 47.428 1.001
res[256] -21.601 16.659 -53.042 -33.062 -21.878 -10.646 12.267 1.001
res[257] 5.310 16.721 -26.340 -6.021 5.033 16.411 39.015 1.001
res[258] 21.015 16.847 -10.852 9.662 20.790 32.193 55.145 1.001
res[259] 57.059 17.037 24.518 45.611 56.831 68.241 92.442 1.002
res[260] 34.481 17.288 1.254 23.094 34.411 45.908 70.086 1.001
res[261] 50.413 17.715 15.780 38.279 50.907 62.488 84.294 1.002
res[262] 1.013 17.462 -32.559 -11.003 1.463 13.068 33.840 1.002
res[263] -13.632 17.268 -46.927 -25.466 -13.251 -1.826 18.917 1.002
res[264] 28.083 17.137 -5.178 16.694 28.340 39.623 60.566 1.003
res[265] 73.774 17.069 40.522 62.477 73.840 85.174 106.109 1.003
res[266] -36.234 17.065 -69.304 -47.505 -35.963 -24.747 -3.793 1.003
res[267] -22.093 17.125 -55.763 -33.330 -21.828 -10.616 10.070 1.003
res[268] 14.160 17.249 -19.827 3.041 14.507 25.776 46.182 1.003
res[269] -59.954 17.435 -93.778 -71.235 -59.514 -48.101 -27.315 1.003
res[270] -22.812 17.681 -57.121 -34.293 -22.324 -10.851 10.918 1.003
res[271] -125.907 17.458 -160.933 -137.188 -125.802 -114.461 -92.053 1.001
res[272] -62.314 17.229 -97.496 -73.416 -62.473 -50.835 -29.085 1.001
res[273] -35.666 17.061 -70.145 -46.545 -35.800 -24.427 -3.232 1.001
res[274] -2.957 16.956 -37.392 -13.883 -2.813 8.075 29.213 1.001
res[275] -9.344 16.916 -43.467 -20.207 -9.343 1.681 22.885 1.001
res[276] 22.554 16.940 -11.628 11.868 22.593 33.645 54.629 1.001
res[277] 73.779 17.029 39.473 63.039 73.780 84.850 106.184 1.001
res[278] 143.908 17.181 109.484 132.820 143.915 155.171 176.723 1.001
res[279] 100.141 17.395 65.573 88.965 100.141 111.576 133.506 1.001
res[280] -46.044 17.669 -80.667 -57.400 -45.955 -34.590 -12.407 1.001
res[281] -5.699 17.595 -39.468 -17.381 -5.770 5.983 28.301 1.001
res[282] 0.419 17.343 -33.174 -10.923 0.288 11.974 34.262 1.001
res[283] -12.869 17.152 -46.211 -24.317 -13.049 -1.401 20.398 1.001
res[284] 12.545 17.023 -20.331 1.056 12.458 24.113 45.686 1.001
res[285] 54.857 16.958 22.320 43.310 54.741 66.049 88.406 1.001
res[286] 12.136 16.958 -20.207 0.644 11.947 23.530 45.348 1.001
res[287] -10.984 17.022 -43.192 -22.616 -10.977 0.294 22.275 1.001
res[288] 4.979 17.150 -27.724 -6.762 5.048 16.454 38.007 1.001
res[289] -29.791 17.340 -62.952 -41.651 -29.779 -18.299 3.958 1.001
res[290] -25.671 17.591 -59.797 -37.708 -25.457 -14.066 8.558 1.001
res[291] 28.550 17.963 -7.697 16.728 28.845 40.812 62.212 1.001
res[292] -9.089 17.712 -45.024 -20.553 -8.933 2.924 24.333 1.001
res[293] -49.732 17.521 -85.124 -61.052 -49.636 -38.060 -16.508 1.001
res[294] -58.677 17.390 -93.259 -69.572 -58.567 -47.134 -25.799 1.001
res[295] -57.955 17.322 -92.707 -68.933 -57.842 -46.344 -25.049 1.001
res[296] -3.734 17.317 -38.668 -14.858 -3.653 7.873 29.033 1.001
res[297] 69.494 17.375 34.053 58.293 69.643 81.139 102.719 1.001
res[298] 42.465 17.496 6.356 31.206 42.578 54.056 75.774 1.001
res[299] 7.231 17.678 -29.387 -4.288 7.395 19.167 40.819 1.001
res[300] -23.337 17.919 -60.558 -34.994 -23.228 -11.302 10.882 1.001
res[301] -51.903 17.982 -88.248 -63.876 -52.309 -39.714 -17.303 1.001
res[302] -37.852 17.747 -73.574 -49.599 -38.337 -25.637 -3.466 1.001
res[303] 9.383 17.571 -25.880 -2.168 9.060 21.337 43.272 1.001
res[304] 6.786 17.457 -27.982 -4.692 6.466 18.794 40.534 1.001
res[305] -83.287 17.404 -117.576 -94.688 -83.511 -71.384 -50.132 1.001
res[306] -56.131 17.415 -90.605 -67.604 -56.382 -44.092 -22.768 1.001
res[307] 29.387 17.488 -5.255 17.630 29.168 41.485 62.770 1.001
res[308] 97.884 17.624 63.110 86.054 97.739 110.020 131.499 1.001
res[309] 53.516 17.820 18.505 41.582 53.468 65.807 87.676 1.001
res[310] -20.057 18.074 -55.492 -32.169 -20.032 -7.574 14.442 1.001
res[311] 101.300 17.549 67.220 89.168 101.137 113.302 135.233 1.001
res[312] 83.175 17.312 49.506 71.360 82.808 95.098 116.774 1.001
res[313] 71.785 17.135 37.980 60.064 71.677 83.600 105.227 1.001
res[314] 88.437 17.022 55.339 76.901 88.506 100.014 122.116 1.001
res[315] -0.110 16.972 -33.336 -11.341 0.071 11.200 33.192 1.001
res[316] -26.794 16.987 -60.411 -38.159 -26.771 -15.599 6.418 1.001
res[317] -88.891 17.067 -122.585 -100.389 -88.824 -77.593 -55.404 1.001
res[318] -96.339 17.209 -130.866 -107.673 -96.328 -84.910 -62.716 1.001
res[319] -61.837 17.414 -96.679 -73.288 -61.840 -50.019 -28.051 1.001
res[320] -108.552 17.679 -143.474 -120.010 -108.694 -96.508 -74.344 1.001
res[321] -74.410 17.625 -109.575 -85.816 -74.485 -62.663 -39.753 1.001
res[322] -41.400 17.380 -75.871 -52.760 -41.519 -29.797 -7.178 1.001
res[323] -74.807 17.196 -108.901 -86.261 -74.760 -63.308 -41.163 1.001
res[324] -45.144 17.074 -79.209 -56.502 -45.026 -33.729 -12.103 1.001
res[325] 4.537 17.016 -29.468 -6.710 4.542 15.856 37.618 1.001
res[326] 59.794 17.022 26.116 48.375 59.758 71.282 93.240 1.001
res[327] 40.165 17.092 6.814 28.767 40.355 51.655 73.479 1.001
res[328] 30.285 17.226 -3.464 18.692 30.679 41.872 63.673 1.001
res[329] 22.589 17.422 -10.860 10.756 23.053 34.110 56.454 1.001
res[330] 92.703 17.678 58.616 80.766 93.284 104.245 126.965 1.001
res[331] 95.283 17.977 59.650 83.167 95.192 107.412 130.221 1.001
res[332] 112.719 17.720 77.424 100.669 112.724 124.693 147.222 1.001
res[333] 70.443 17.522 35.436 58.422 70.438 82.385 104.268 1.001
res[334] 69.514 17.384 34.563 57.587 69.353 81.410 102.556 1.001
res[335] 70.134 17.309 35.643 58.219 69.855 81.817 103.521 1.001
res[336] -1.755 17.297 -35.726 -13.635 -1.976 10.018 31.941 1.001
res[337] -93.736 17.349 -127.604 -105.548 -93.768 -81.835 -60.000 1.001
res[338] -48.951 17.463 -82.779 -60.869 -49.029 -36.839 -14.994 1.001
res[339] -121.819 17.638 -156.071 -133.910 -122.015 -109.591 -87.286 1.001
res[340] -103.701 17.874 -138.279 -115.672 -103.713 -91.305 -68.978 1.001
res[341] -69.317 18.059 -103.485 -81.639 -69.415 -57.406 -33.457 1.001
res[342] -32.346 17.788 -65.785 -44.511 -32.362 -20.467 2.839 1.001
res[343] -21.629 17.575 -54.850 -33.597 -21.808 -9.882 13.449 1.001
res[344] -59.307 17.422 -92.307 -71.080 -59.415 -47.483 -24.425 1.001
res[345] -3.627 17.331 -36.621 -15.370 -3.984 8.092 31.060 1.001
res[346] 78.394 17.304 46.202 66.537 78.021 90.261 112.620 1.001
res[347] 100.999 17.339 68.667 89.254 100.770 113.032 135.290 1.001
res[348] -22.296 17.438 -55.281 -34.095 -22.507 -10.328 12.264 1.001
res[349] 46.092 17.598 12.847 34.241 46.001 58.157 80.422 1.001
res[350] 27.883 17.819 -5.915 15.648 27.735 40.121 63.077 1.001
sigma 55.917 2.244 51.705 54.351 55.829 57.468 60.369 1.003
sigma.B 64.474 8.406 50.251 58.466 63.695 69.675 83.144 1.006
deviance 3809.753 9.145 3794.047 3803.114 3809.077 3815.608 3829.461 1.003
n.eff
beta 3000
beta0 3000
gamma[1] 1800
gamma[2] 3000
gamma[3] 2100
gamma[4] 3000
gamma[5] 3000
gamma[6] 3000
gamma[7] 3000
gamma[8] 3000
gamma[9] 2800
gamma[10] 3000
gamma[11] 2100
gamma[12] 3000
gamma[13] 3000
gamma[14] 3000
gamma[15] 2500
gamma[16] 1700
gamma[17] 1700
gamma[18] 1800
gamma[19] 3000
gamma[20] 1500
gamma[21] 3000
gamma[22] 3000
gamma[23] 3000
gamma[24] 3000
gamma[25] 3000
gamma[26] 1700
gamma[27] 1500
gamma[28] 3000
gamma[29] 2300
gamma[30] 3000
gamma[31] 3000
gamma[32] 3000
gamma[33] 2500
gamma[34] 3000
gamma[35] 3000
res[1] 1100
res[2] 1000
res[3] 990
res[4] 940
res[5] 910
res[6] 880
res[7] 860
res[8] 850
res[9] 840
res[10] 840
res[11] 3000
res[12] 3000
res[13] 3000
res[14] 3000
res[15] 3000
res[16] 3000
res[17] 3000
res[18] 3000
res[19] 3000
res[20] 3000
res[21] 1200
res[22] 1200
res[23] 1100
res[24] 1000
res[25] 1000
res[26] 970
res[27] 950
res[28] 1200
res[29] 920
res[30] 920
res[31] 3000
res[32] 3000
res[33] 3000
res[34] 3000
res[35] 3000
res[36] 3000
res[37] 3000
res[38] 3000
res[39] 3000
res[40] 3000
res[41] 3000
res[42] 3000
res[43] 3000
res[44] 3000
res[45] 3000
res[46] 3000
res[47] 3000
res[48] 3000
res[49] 3000
res[50] 3000
res[51] 3000
res[52] 3000
res[53] 3000
res[54] 3000
res[55] 3000
res[56] 3000
res[57] 3000
res[58] 3000
res[59] 3000
res[60] 3000
res[61] 3000
res[62] 3000
res[63] 3000
res[64] 3000
res[65] 3000
res[66] 3000
res[67] 3000
res[68] 3000
res[69] 3000
res[70] 3000
res[71] 3000
res[72] 3000
res[73] 3000
res[74] 3000
res[75] 3000
res[76] 3000
res[77] 3000
res[78] 3000
res[79] 3000
res[80] 3000
res[81] 1100
res[82] 1100
res[83] 1000
res[84] 970
res[85] 930
res[86] 930
res[87] 1100
res[88] 860
res[89] 850
res[90] 850
res[91] 3000
res[92] 3000
res[93] 3000
res[94] 3000
res[95] 3000
res[96] 3000
res[97] 3000
res[98] 3000
res[99] 3000
res[100] 3000
res[101] 2700
res[102] 2700
res[103] 2800
res[104] 3000
res[105] 3000
res[106] 3000
res[107] 3000
res[108] 3000
res[109] 3000
res[110] 3000
res[111] 3000
res[112] 3000
res[113] 3000
res[114] 3000
res[115] 3000
res[116] 3000
res[117] 3000
res[118] 3000
res[119] 3000
res[120] 3000
res[121] 3000
res[122] 3000
res[123] 3000
res[124] 3000
res[125] 3000
res[126] 3000
res[127] 3000
res[128] 3000
res[129] 3000
res[130] 3000
res[131] 3000
res[132] 3000
res[133] 3000
res[134] 3000
res[135] 3000
res[136] 3000
res[137] 3000
res[138] 3000
res[139] 3000
res[140] 3000
res[141] 2700
res[142] 2700
res[143] 2800
res[144] 3000
res[145] 3000
res[146] 3000
res[147] 3000
res[148] 3000
res[149] 3000
res[150] 3000
res[151] 1700
res[152] 2200
res[153] 2300
res[154] 1900
res[155] 1900
res[156] 2000
res[157] 2200
res[158] 2300
res[159] 2500
res[160] 2700
res[161] 1500
res[162] 1500
res[163] 1500
res[164] 1000
res[165] 1600
res[166] 1700
res[167] 1800
res[168] 1900
res[169] 2000
res[170] 1600
res[171] 3000
res[172] 1900
res[173] 1900
res[174] 2000
res[175] 2000
res[176] 2100
res[177] 2300
res[178] 2400
res[179] 2600
res[180] 2800
res[181] 3000
res[182] 3000
res[183] 3000
res[184] 3000
res[185] 3000
res[186] 3000
res[187] 3000
res[188] 3000
res[189] 3000
res[190] 3000
res[191] 1500
res[192] 630
res[193] 570
res[194] 1600
res[195] 1700
res[196] 1800
res[197] 1900
res[198] 2000
res[199] 2100
res[200] 2300
res[201] 3000
res[202] 3000
res[203] 3000
res[204] 3000
res[205] 3000
res[206] 3000
res[207] 3000
res[208] 3000
res[209] 3000
res[210] 3000
res[211] 2000
res[212] 1900
res[213] 1700
res[214] 1600
res[215] 1600
res[216] 1700
res[217] 1700
res[218] 1900
res[219] 1400
res[220] 1400
res[221] 3000
res[222] 3000
res[223] 3000
res[224] 3000
res[225] 3000
res[226] 3000
res[227] 3000
res[228] 3000
res[229] 3000
res[230] 3000
res[231] 3000
res[232] 3000
res[233] 3000
res[234] 3000
res[235] 3000
res[236] 3000
res[237] 3000
res[238] 3000
res[239] 3000
res[240] 3000
res[241] 3000
res[242] 3000
res[243] 3000
res[244] 3000
res[245] 3000
res[246] 3000
res[247] 3000
res[248] 3000
res[249] 3000
res[250] 3000
res[251] 1800
res[252] 1800
res[253] 1900
res[254] 1900
res[255] 2000
res[256] 2100
res[257] 2200
res[258] 2400
res[259] 3000
res[260] 2800
res[261] 930
res[262] 880
res[263] 830
res[264] 790
res[265] 750
res[266] 740
res[267] 720
res[268] 710
res[269] 710
res[270] 710
res[271] 3000
res[272] 3000
res[273] 3000
res[274] 3000
res[275] 3000
res[276] 3000
res[277] 3000
res[278] 3000
res[279] 3000
res[280] 3000
res[281] 2600
res[282] 2600
res[283] 2700
res[284] 2800
res[285] 3000
res[286] 3000
res[287] 3000
res[288] 3000
res[289] 3000
res[290] 3000
res[291] 3000
res[292] 3000
res[293] 3000
res[294] 3000
res[295] 3000
res[296] 3000
res[297] 3000
res[298] 3000
res[299] 3000
res[300] 3000
res[301] 3000
res[302] 3000
res[303] 3000
res[304] 3000
res[305] 3000
res[306] 3000
res[307] 3000
res[308] 3000
res[309] 3000
res[310] 3000
res[311] 3000
res[312] 3000
res[313] 3000
res[314] 3000
res[315] 3000
res[316] 3000
res[317] 3000
res[318] 3000
res[319] 3000
res[320] 3000
res[321] 2700
res[322] 2800
res[323] 2900
res[324] 3000
res[325] 3000
res[326] 3000
res[327] 3000
res[328] 3000
res[329] 3000
res[330] 3000
res[331] 3000
res[332] 3000
res[333] 3000
res[334] 3000
res[335] 3000
res[336] 3000
res[337] 3000
res[338] 3000
res[339] 3000
res[340] 3000
res[341] 3000
res[342] 3000
res[343] 3000
res[344] 3000
res[345] 3000
res[346] 3000
res[347] 3000
res[348] 3000
res[349] 3000
res[350] 3000
sigma 700
sigma.B 1000
deviance 720
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 41.8 and DIC = 3851.5
DIC is an estimate of expected predictive error (lower deviance is better).Matrix parameterisation
> modelString2="
+ model {
+ #Likelihood
+ for (i in 1:n) {
+ y[i]~dnorm(mu[i],tau)
+ mu[i] <- inprod(beta[],X[i,]) + gamma[Block[i]]
+ res[i] <- y[i]-mu[i]
+ }
+
+ #Priors
+ beta ~ dmnorm(a0,A0)
+ for (i in 1:nBlock) {
+ gamma[i] ~ dnorm(0, tau.B) #prior
+ }
+ tau <- pow(sigma,-2)
+ sigma <- z/sqrt(chSq)
+ z ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq ~ dgamma(0.5, 0.5)
+
+ tau.B <- pow(sigma.B,-2)
+ sigma.B <- z/sqrt(chSq.B)
+ z.B ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq.B ~ dgamma(0.5, 0.5)
+ }
+ "
>
> ## write the model to a text file
> writeLines(modelString2, con = "matrixModel2.txt")
>
> Xmat <- model.matrix(~Time,data.rm)
> data.rm.list <- with(data.rm,
+ list(y=y,
+ Block=as.numeric(Block),
+ X=Xmat,
+ n=nrow(data.rm),
+ nBlock=length(levels(Block)),
+ a0=rep(0,ncol(Xmat)), A0=diag(ncol(Xmat))
+ )
+ )
>
> params <- c("beta",'gamma',"sigma","sigma.B","res")
> adaptSteps = 1000
> burnInSteps = 3000
> nChains = 2
> numSavedSteps = 3000
> thinSteps = 1
> nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains)
>
> data.rm.r2jags.m <- jags(data = data.rm.list, inits = NULL, parameters.to.save = params,
+ model.file = "matrixModel2.txt", n.chains = nChains, n.iter = nIter,
+ n.burnin = burnInSteps, n.thin = thinSteps)
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 350
Unobserved stochastic nodes: 40
Total graph size: 2521
Initializing model
>
> print(data.rm.r2jags.m)
Inference for Bugs model at "matrixModel2.txt", fit using jags,
2 chains, each with 4500 iterations (first 3000 discarded)
n.sims = 3000 iterations saved
mu.vect sd.vect 2.5% 25% 50% 75% 97.5% Rhat
beta[1] 0.118 0.993 -1.825 -0.560 0.127 0.772 2.136 1.002
beta[2] 9.067 1.041 6.989 8.384 9.085 9.754 11.096 1.009
gamma[1] 268.496 28.003 214.165 249.963 268.515 287.365 322.199 1.002
gamma[2] 249.357 27.207 196.523 230.541 249.374 268.093 303.009 1.001
gamma[3] 326.337 28.472 271.718 306.769 325.694 345.668 383.423 1.002
gamma[4] 305.015 28.782 249.411 285.199 305.040 324.243 361.356 1.001
gamma[5] 377.709 27.831 324.335 358.940 377.037 396.616 432.150 1.001
gamma[6] 343.430 27.578 288.864 325.843 342.939 361.444 396.819 1.001
gamma[7] 332.166 27.783 278.248 313.377 331.664 351.388 385.777 1.002
gamma[8] 271.616 27.163 217.184 253.588 271.956 289.628 322.963 1.001
gamma[9] 384.589 27.386 332.007 366.136 384.502 402.093 440.209 1.001
gamma[10] 367.756 27.587 314.137 349.123 368.026 386.501 421.707 1.001
gamma[11] 457.715 27.438 405.652 439.504 457.268 476.098 513.423 1.001
gamma[12] 312.867 27.216 262.216 293.798 313.154 331.284 366.377 1.001
gamma[13] 258.804 27.818 201.324 240.475 259.644 276.264 313.330 1.002
gamma[14] 279.449 28.042 224.175 260.014 279.067 298.411 335.404 1.001
gamma[15] 337.363 28.099 284.866 317.715 336.998 356.109 394.348 1.001
gamma[16] 416.383 27.354 363.925 397.826 416.595 434.011 473.215 1.002
gamma[17] 403.080 27.501 349.003 384.921 403.079 421.627 456.974 1.002
gamma[18] 237.418 27.946 183.713 218.161 237.435 256.648 290.420 1.001
gamma[19] 323.886 27.728 270.777 305.233 323.114 342.641 377.533 1.001
gamma[20] 275.462 28.013 220.684 255.987 275.838 294.317 330.957 1.001
gamma[21] 194.059 27.398 141.539 175.756 194.167 211.807 248.181 1.002
gamma[22] 289.821 27.693 236.092 271.210 289.707 307.332 344.403 1.001
gamma[23] 217.663 28.050 164.441 197.887 217.932 235.812 274.184 1.002
gamma[24] 212.748 27.923 159.816 193.937 211.567 231.708 268.892 1.001
gamma[25] 255.843 26.839 204.539 237.181 255.916 274.542 309.265 1.003
gamma[26] 206.396 28.055 152.547 187.160 206.227 225.611 261.170 1.001
gamma[27] 327.559 27.486 273.350 309.633 327.509 345.364 380.375 1.002
gamma[28] 384.714 27.705 330.300 365.884 384.552 403.155 437.847 1.003
gamma[29] 304.783 28.077 251.111 284.961 304.255 323.437 360.045 1.001
gamma[30] 225.251 28.017 168.742 206.532 226.000 243.944 279.897 1.001
gamma[31] 242.036 28.513 184.632 223.534 242.114 260.552 297.438 1.001
gamma[32] 250.059 27.603 197.965 231.432 249.373 268.506 305.275 1.003
gamma[33] 321.386 27.863 266.714 302.647 321.462 340.165 377.552 1.003
gamma[34] 368.704 27.907 314.047 350.229 368.434 387.452 423.293 1.001
gamma[35] 365.968 27.738 311.338 347.444 365.930 385.018 420.415 1.005
res[1] 4.433 27.784 -48.877 -14.717 4.562 22.705 58.869 1.002
res[2] 34.393 27.628 -18.119 15.474 34.478 52.583 88.788 1.002
res[3] -17.044 27.510 -69.264 -35.707 -16.883 0.972 37.088 1.002
res[4] -19.010 27.431 -70.907 -37.537 -18.756 -0.634 35.109 1.002
res[5] 22.692 27.391 -29.376 4.107 22.942 41.160 77.308 1.001
res[6] 10.582 27.391 -41.038 -7.968 10.837 28.907 65.778 1.001
res[7] -70.449 27.431 -121.778 -88.991 -69.960 -52.214 -14.834 1.001
res[8] 21.008 27.509 -30.615 2.408 21.241 39.197 76.881 1.001
res[9] 12.673 27.627 -39.023 -6.003 12.972 31.145 68.777 1.001
res[10] 22.988 27.783 -29.250 4.168 22.937 41.683 79.296 1.001
res[11] -40.986 26.942 -94.515 -59.717 -41.262 -22.608 11.356 1.001
res[12] -57.652 26.765 -110.392 -76.201 -57.806 -39.438 -5.452 1.001
res[13] 14.195 26.627 -37.606 -4.203 14.145 32.218 66.504 1.001
res[14] -29.460 26.529 -81.001 -47.601 -29.683 -11.482 22.755 1.001
res[15] -14.892 26.472 -66.711 -32.886 -15.051 3.149 37.784 1.001
res[16] 15.000 26.456 -36.965 -3.255 14.703 33.011 68.048 1.001
res[17] -11.656 26.481 -63.530 -29.872 -12.202 6.352 41.041 1.001
res[18] -2.098 26.546 -53.836 -20.736 -2.884 15.886 51.209 1.001
res[19] 40.030 26.652 -11.158 21.366 39.102 58.171 93.729 1.001
res[20] 112.896 26.799 61.236 94.306 112.162 131.227 167.261 1.001
res[21] -173.333 28.266 -230.343 -192.502 -172.496 -153.934 -119.008 1.002
res[22] -146.973 28.095 -203.369 -166.084 -146.394 -127.937 -93.044 1.002
res[23] -66.390 27.961 -122.215 -85.409 -65.713 -47.492 -12.298 1.002
res[24] -62.498 27.865 -117.833 -81.428 -61.625 -43.630 -7.786 1.001
res[25] -16.892 27.808 -71.818 -35.704 -16.206 2.104 37.863 1.001
res[26] 37.026 27.790 -17.773 18.140 37.505 55.996 91.643 1.001
res[27] 73.127 27.811 18.616 54.532 73.671 91.725 127.823 1.001
res[28] 125.466 27.871 71.518 106.855 125.737 144.036 180.266 1.001
res[29] 132.725 27.969 78.584 113.924 133.004 151.381 187.753 1.001
res[30] 128.171 28.106 73.520 109.247 128.243 147.168 184.155 1.001
res[31] -215.417 28.519 -271.907 -234.515 -215.477 -196.031 -160.014 1.001
res[32] -172.464 28.331 -228.398 -191.559 -172.626 -153.223 -117.470 1.001
res[33] -107.754 28.180 -163.519 -126.542 -107.988 -88.710 -53.225 1.001
res[34] -46.543 28.067 -102.122 -65.407 -46.791 -27.844 8.278 1.001
res[35] -47.922 27.992 -103.460 -66.793 -48.157 -29.112 7.029 1.001
res[36] 71.901 27.955 16.630 52.816 71.633 90.451 126.471 1.001
res[37] 97.292 27.958 42.344 78.098 97.282 115.785 151.917 1.001
res[38] 113.786 27.999 59.110 94.749 113.857 132.397 169.334 1.001
res[39] 188.465 28.078 134.278 169.268 188.455 207.026 244.767 1.001
res[40] 152.859 28.196 98.827 133.783 152.725 171.438 209.588 1.001
res[41] -138.298 27.589 -192.214 -157.018 -137.668 -119.884 -85.511 1.001
res[42] -0.435 27.414 -54.092 -19.066 0.070 17.947 51.755 1.001
res[43] -5.275 27.278 -58.296 -23.835 -4.661 12.955 46.693 1.001
res[44] 76.163 27.182 23.390 57.931 76.757 94.384 128.160 1.001
res[45] -8.105 27.124 -60.470 -26.335 -7.526 10.317 43.968 1.001
res[46] -8.933 27.107 -61.592 -27.005 -8.421 9.419 43.130 1.001
res[47] 23.039 27.130 -29.532 5.000 23.698 41.485 75.548 1.001
res[48] 48.884 27.192 -3.759 30.945 49.511 67.086 101.297 1.001
res[49] 8.462 27.295 -44.134 -9.630 8.812 26.700 61.215 1.001
res[50] 31.557 27.436 -20.973 13.381 31.746 50.020 84.424 1.001
res[51] -128.097 27.415 -180.770 -146.327 -127.910 -110.576 -73.568 1.001
res[52] -60.141 27.254 -112.252 -78.239 -59.732 -42.653 -5.561 1.001
res[53] 17.013 27.132 -35.210 -1.266 17.578 34.265 71.525 1.001
res[54] -82.564 27.049 -134.784 -100.658 -82.293 -65.282 -27.984 1.002
res[55] 14.994 27.006 -36.578 -3.173 15.282 32.302 69.851 1.002
res[56] -26.609 27.004 -78.326 -44.704 -26.580 -9.314 28.128 1.002
res[57] 29.085 27.041 -22.987 10.998 29.221 46.243 83.856 1.002
res[58] 88.084 27.118 35.657 69.858 88.230 105.263 142.463 1.004
res[59] 96.481 27.235 43.718 78.058 96.354 113.557 150.554 1.004
res[60] 85.123 27.391 32.058 66.554 85.013 102.661 139.651 1.005
res[61] -114.949 27.627 -168.618 -134.296 -114.394 -96.450 -60.949 1.001
res[62] -68.590 27.512 -121.492 -87.723 -68.056 -50.063 -14.649 1.001
res[63] -5.091 27.435 -57.658 -24.187 -4.767 13.171 48.423 1.001
res[64] -96.888 27.399 -149.185 -115.932 -96.721 -78.893 -43.557 1.001
res[65] -145.340 27.401 -197.553 -164.388 -145.424 -127.432 -91.411 1.001
res[66] -26.577 27.444 -78.399 -45.694 -26.594 -8.455 27.555 1.001
res[67] 53.432 27.525 1.678 34.253 53.095 71.854 107.546 1.001
res[68] 91.059 27.646 39.251 71.830 90.780 109.558 145.538 1.003
res[69] 139.341 27.805 87.022 120.095 138.966 157.961 193.921 1.001
res[70] 192.254 28.001 139.613 173.011 191.889 211.174 247.685 1.001
res[71] -140.697 26.945 -192.131 -158.462 -140.921 -122.682 -86.498 1.001
res[72] -53.861 26.803 -104.692 -71.382 -53.867 -36.045 -0.026 1.001
res[73] -59.969 26.701 -110.888 -77.531 -60.116 -42.419 -5.779 1.001
res[74] -24.888 26.639 -75.800 -42.339 -25.220 -7.759 28.792 1.001
res[75] -18.925 26.617 -70.569 -36.419 -19.228 -1.820 34.501 1.001
res[76] 48.388 26.637 -3.281 30.722 48.168 65.796 102.013 1.001
res[77] 45.403 26.697 -6.795 27.656 45.293 62.830 99.324 1.001
res[78] 90.550 26.797 38.062 72.851 90.464 108.076 144.636 1.001
res[79] 85.396 26.937 32.309 67.374 84.992 103.181 139.994 1.001
res[80] 50.353 27.116 -2.874 32.360 50.071 68.275 105.635 1.001
res[81] -163.315 27.183 -218.512 -180.651 -163.268 -145.149 -111.213 1.001
res[82] -109.549 27.050 -164.522 -126.836 -109.407 -91.446 -57.185 1.001
res[83] -13.182 26.957 -68.058 -30.309 -13.185 4.672 38.759 1.001
res[84] -14.857 26.904 -69.375 -32.207 -15.130 2.965 37.149 1.001
res[85] 40.982 26.891 -12.987 23.736 40.580 58.715 93.178 1.001
res[86] 132.360 26.918 78.198 115.020 131.926 150.358 184.466 1.001
res[87] 96.805 26.986 42.362 79.456 96.215 114.807 149.347 1.001
res[88] 20.474 27.093 -33.942 3.067 19.924 38.470 72.341 1.001
res[89] 17.776 27.240 -36.170 0.154 17.205 35.757 69.869 1.001
res[90] 21.069 27.426 -33.512 3.375 20.566 38.921 73.507 1.001
res[91] -139.087 27.401 -192.251 -157.857 -139.429 -120.731 -85.751 1.001
res[92] -36.783 27.249 -89.549 -55.363 -37.012 -18.606 16.371 1.001
res[93] -52.676 27.136 -105.357 -71.142 -52.862 -34.505 0.149 1.001
res[94] -26.246 27.062 -78.812 -44.487 -26.694 -8.200 27.216 1.001
res[95] -30.949 27.028 -83.569 -49.064 -31.432 -12.883 22.822 1.001
res[96] -18.119 27.035 -70.366 -36.181 -18.630 -0.071 35.799 1.001
res[97] 11.013 27.081 -42.062 -7.308 10.371 29.090 64.960 1.001
res[98] 89.212 27.167 36.723 70.825 88.487 107.474 143.357 1.001
res[99] 95.614 27.293 43.369 77.242 94.962 114.096 150.199 1.001
res[100] 134.498 27.457 80.966 116.052 134.051 153.002 189.417 1.001
res[101] -76.108 27.204 -130.082 -94.332 -75.847 -57.878 -24.353 1.001
res[102] -34.250 27.032 -87.681 -52.048 -34.152 -16.151 17.341 1.001
res[103] -71.035 26.900 -124.029 -88.589 -71.012 -53.026 -19.557 1.001
res[104] 13.787 26.807 -38.887 -3.638 13.685 31.994 65.003 1.001
res[105] -14.560 26.754 -67.146 -32.253 -14.734 3.512 36.383 1.001
res[106] -19.293 26.742 -72.025 -36.855 -19.308 -1.263 32.398 1.001
res[107] 56.600 26.770 3.888 38.981 56.413 74.590 108.690 1.001
res[108] 116.002 26.839 62.639 98.370 115.911 133.987 168.211 1.001
res[109] 48.507 26.948 -4.467 30.803 48.406 66.425 100.281 1.001
res[110] 9.543 27.096 -43.482 -8.442 9.395 27.710 61.257 1.001
res[111] -132.106 27.068 -185.510 -150.360 -132.361 -113.290 -81.768 1.002
res[112] -91.911 26.941 -144.896 -110.112 -92.368 -73.497 -41.675 1.002
res[113] -56.418 26.853 -110.121 -74.546 -56.821 -38.144 -6.066 1.002
res[114] -13.873 26.805 -66.754 -32.098 -14.064 4.250 36.754 1.002
res[115] 33.751 26.798 -19.527 15.438 33.439 51.710 84.504 1.002
res[116] 18.335 26.831 -34.945 -0.042 17.997 36.508 69.231 1.003
res[117] -9.402 26.904 -62.947 -27.827 -9.801 8.739 41.996 1.003
res[118] 73.620 27.018 20.102 55.043 73.349 91.735 125.589 1.003
res[119] 130.437 27.170 77.165 111.769 130.243 148.448 183.288 1.003
res[120] 67.067 27.362 14.395 48.375 66.985 85.315 120.963 1.004
res[121] -62.784 27.602 -117.124 -80.547 -63.554 -44.541 -5.745 1.002
res[122] -79.284 27.432 -132.901 -96.959 -80.152 -61.213 -23.216 1.002
res[123] -147.038 27.300 -200.594 -164.755 -147.987 -129.337 -91.122 1.002
res[124] -86.011 27.208 -139.363 -103.583 -87.079 -68.166 -30.561 1.001
res[125] -44.469 27.155 -96.901 -61.934 -45.519 -26.882 10.835 1.001
res[126] -7.957 27.143 -60.233 -25.501 -9.007 9.627 47.109 1.001
res[127] 41.116 27.170 -10.769 23.449 40.140 58.470 96.951 1.001
res[128] 117.876 27.237 66.278 99.824 117.103 135.377 173.458 1.003
res[129] 149.628 27.343 98.060 131.402 148.903 167.283 205.474 1.002
res[130] 138.114 27.489 85.817 119.560 137.512 155.791 194.856 1.002
res[131] -111.510 27.838 -167.229 -130.194 -111.277 -92.014 -56.583 1.002
res[132] -85.928 27.671 -141.664 -104.693 -85.568 -66.741 -30.867 1.002
res[133] -39.184 27.543 -95.068 -57.826 -39.100 -20.158 15.452 1.002
res[134] -65.087 27.454 -120.528 -83.757 -65.031 -46.398 -10.806 1.002
res[135] -38.854 27.404 -94.235 -57.313 -38.905 -20.233 15.932 1.002
res[136] 43.897 27.394 -11.085 25.502 43.662 62.725 99.335 1.002
res[137] 60.508 27.423 5.661 42.259 60.002 79.149 116.033 1.002
res[138] 48.476 27.491 -6.511 30.204 47.961 67.171 103.838 1.002
res[139] 64.161 27.599 9.521 45.658 63.389 82.927 119.918 1.002
res[140] 150.425 27.745 95.799 131.748 149.642 169.252 206.380 1.003
res[141] -91.850 27.881 -148.268 -110.602 -91.492 -72.233 -39.029 1.001
res[142] -17.357 27.708 -73.303 -36.036 -17.162 1.868 35.260 1.001
res[143] -8.456 27.572 -63.972 -27.298 -8.090 10.649 43.948 1.001
res[144] 16.411 27.476 -38.675 -2.242 16.566 35.463 68.828 1.001
res[145] -7.945 27.418 -62.620 -26.453 -7.775 11.028 44.009 1.001
res[146] 34.948 27.400 -19.537 16.194 35.119 53.767 87.148 1.001
res[147] 17.864 27.422 -36.519 -0.769 17.959 36.562 70.397 1.001
res[148] -37.328 27.483 -92.124 -55.967 -37.389 -18.410 15.393 1.001
res[149] 0.133 27.583 -54.930 -18.289 0.029 18.855 53.369 1.001
res[150] 125.181 27.722 69.744 106.772 124.931 144.185 179.294 1.001
res[151] -45.913 27.112 -101.600 -63.384 -46.504 -27.406 6.233 1.002
res[152] 14.074 26.949 -41.422 -3.190 13.364 32.310 66.645 1.001
res[153] 25.930 26.825 -28.692 8.617 25.258 43.842 78.335 1.001
res[154] -8.769 26.741 -62.803 -25.915 -9.134 8.810 43.512 1.001
res[155] -12.026 26.698 -66.536 -29.146 -12.358 5.538 40.695 1.001
res[156] -13.996 26.695 -68.442 -31.190 -14.374 3.511 39.057 1.001
res[157] -21.157 26.732 -75.444 -38.415 -21.645 -3.442 32.176 1.001
res[158] 35.944 26.810 -17.938 18.462 35.409 53.573 89.820 1.001
res[159] -9.265 26.928 -63.044 -26.958 -9.879 8.560 44.932 1.001
res[160] 61.941 27.086 8.272 44.148 61.146 79.841 116.112 1.001
res[161] -111.720 27.299 -164.219 -130.281 -111.941 -93.352 -57.961 1.002
res[162] -161.840 27.142 -214.803 -180.270 -162.077 -143.321 -108.335 1.002
res[163] -105.843 27.025 -158.096 -124.374 -106.136 -87.584 -52.496 1.002
res[164] 32.678 26.947 -18.932 14.279 32.115 50.832 85.368 1.002
res[165] -1.691 26.909 -53.352 -20.188 -2.310 16.517 51.266 1.002
res[166] 45.107 26.912 -6.211 26.808 44.518 63.279 97.999 1.002
res[167] 5.376 26.954 -46.126 -12.677 4.882 23.392 58.513 1.002
res[168] 72.424 27.037 20.741 54.308 72.204 90.456 125.956 1.002
res[169] 87.205 27.159 35.982 68.965 87.205 105.288 141.275 1.002
res[170] 173.321 27.321 121.880 155.039 173.059 191.695 228.030 1.003
res[171] -26.750 27.741 -79.583 -45.635 -26.886 -7.432 26.470 1.001
res[172] -18.152 27.612 -70.442 -37.010 -18.270 0.993 35.150 1.001
res[173] -30.868 27.522 -82.411 -49.842 -30.897 -11.752 22.359 1.001
res[174] -20.371 27.471 -72.112 -39.216 -20.399 -1.090 32.975 1.001
res[175] -29.402 27.460 -81.284 -48.575 -29.553 -9.855 23.536 1.001
res[176] -42.654 27.488 -94.488 -61.958 -42.932 -23.151 10.118 1.001
res[177] 21.559 27.555 -30.491 2.158 21.213 40.881 74.590 1.001
res[178] -6.198 27.662 -58.988 -25.815 -6.244 13.036 47.593 1.001
res[179] 104.363 27.807 51.627 84.332 104.497 123.625 158.553 1.001
res[180] 63.487 27.989 10.897 43.415 63.657 82.927 118.256 1.002
res[181] -116.426 27.477 -170.058 -135.254 -115.973 -98.040 -63.859 1.001
res[182] -61.964 27.315 -115.028 -80.596 -61.367 -43.741 -8.748 1.001
res[183] -11.520 27.191 -65.196 -29.915 -10.904 6.736 41.954 1.001
res[184] -11.403 27.107 -64.157 -29.928 -10.938 7.033 42.438 1.001
res[185] 11.940 27.063 -40.738 -6.618 12.599 30.143 65.828 1.001
res[186] 78.890 27.059 26.180 60.481 79.578 97.004 132.471 1.001
res[187] 15.749 27.094 -36.961 -2.786 16.169 33.923 68.912 1.001
res[188] 3.160 27.170 -49.311 -15.573 3.325 21.357 56.992 1.001
res[189] 52.382 27.285 -0.331 33.687 52.699 70.616 106.503 1.001
res[190] 57.688 27.439 4.937 38.848 57.982 75.882 112.335 1.001
res[191] -39.277 27.823 -93.946 -58.037 -39.479 -19.984 14.965 1.001
res[192] 9.409 27.662 -44.962 -9.063 9.312 28.464 63.569 1.001
res[193] 22.489 27.540 -32.351 3.890 22.479 41.387 76.748 1.001
res[194] -41.856 27.457 -96.305 -60.387 -41.784 -23.180 12.866 1.001
res[195] -12.452 27.413 -66.510 -31.155 -12.405 6.113 42.359 1.001
res[196] -1.869 27.408 -55.985 -20.561 -1.913 16.685 53.271 1.001
res[197] 21.489 27.443 -32.127 2.711 21.389 39.871 76.814 1.001
res[198] -9.600 27.518 -62.931 -28.632 -9.617 8.338 45.590 1.002
res[199] 53.727 27.631 -0.059 34.427 53.676 71.736 108.974 1.002
res[200] 31.695 27.783 -22.231 12.143 31.743 49.979 87.523 1.002
res[201] -86.890 27.181 -140.177 -104.770 -87.118 -68.603 -35.106 1.001
res[202] -30.563 27.031 -83.642 -48.350 -31.011 -12.345 20.910 1.002
res[203] -39.562 26.920 -92.523 -57.243 -39.987 -21.390 11.887 1.002
res[204] 25.751 26.850 -27.313 8.074 25.467 43.881 77.877 1.002
res[205] -12.787 26.819 -65.884 -30.405 -13.246 5.237 39.562 1.002
res[206] -114.094 26.829 -166.864 -131.854 -114.195 -96.423 -61.166 1.002
res[207] -27.215 26.880 -80.040 -44.971 -27.431 -9.544 26.079 1.002
res[208] 65.253 26.970 12.034 47.409 65.333 82.874 119.333 1.002
res[209] 87.094 27.100 33.577 69.194 87.081 104.945 141.467 1.003
res[210] 148.253 27.269 94.421 130.305 148.113 166.284 203.466 1.002
res[211] -161.236 27.503 -215.889 -178.736 -161.122 -142.886 -108.375 1.001
res[212] -129.522 27.348 -183.477 -146.819 -129.294 -111.282 -76.871 1.001
res[213] -190.682 27.231 -243.930 -208.062 -190.524 -172.562 -138.450 1.001
res[214] -79.289 27.154 -132.322 -96.647 -79.209 -61.143 -27.250 1.001
res[215] 47.949 27.116 -4.985 30.474 48.166 66.107 100.695 1.001
res[216] 114.631 27.119 61.912 96.825 114.839 132.864 167.496 1.001
res[217] 117.095 27.161 63.624 99.215 117.216 135.276 169.783 1.001
res[218] 122.954 27.243 68.976 105.183 123.040 140.999 175.833 1.001
res[219] 57.691 27.364 2.985 40.012 57.620 75.929 110.855 1.001
res[220] 124.990 27.525 70.453 107.235 124.767 143.105 178.606 1.001
res[221] -28.457 27.809 -85.147 -46.709 -28.877 -8.749 24.203 1.001
res[222] -40.195 27.642 -96.634 -58.154 -40.465 -20.895 12.714 1.001
res[223] -83.163 27.513 -139.662 -101.235 -83.213 -63.910 -30.005 1.001
res[224] -57.737 27.424 -113.878 -75.793 -57.651 -38.683 -5.179 1.001
res[225] -60.675 27.373 -116.422 -78.560 -60.376 -41.718 -8.273 1.001
res[226] -36.237 27.363 -91.706 -54.143 -35.975 -17.495 16.397 1.001
res[227] -53.528 27.391 -108.591 -71.787 -53.313 -34.530 -0.302 1.001
res[228] 82.085 27.460 27.176 63.546 82.505 100.972 135.212 1.001
res[229] 109.582 27.567 54.642 90.994 110.106 128.598 162.713 1.001
res[230] 190.314 27.713 135.634 171.529 190.765 209.465 244.223 1.001
res[231] -120.252 27.694 -175.928 -138.875 -119.474 -101.313 -68.003 1.001
res[232] -100.688 27.530 -155.801 -119.226 -99.978 -81.979 -48.238 1.001
res[233] -91.964 27.405 -146.450 -110.666 -91.280 -73.148 -39.619 1.001
res[234] -108.171 27.319 -162.489 -126.710 -107.330 -89.436 -55.884 1.001
res[235] 21.527 27.273 -32.755 3.074 22.292 40.459 73.543 1.001
res[236] -18.622 27.266 -73.068 -36.988 -18.139 0.348 33.406 1.001
res[237] 40.129 27.299 -14.569 21.865 40.523 59.257 92.027 1.001
res[238] 117.718 27.372 62.996 99.591 118.175 136.830 169.568 1.001
res[239] 150.564 27.484 95.949 132.308 150.955 169.833 203.577 1.001
res[240] 128.355 27.634 73.287 109.633 128.714 147.821 181.492 1.001
res[241] -43.717 26.592 -96.442 -61.945 -43.778 -25.366 7.706 1.002
res[242] -16.266 26.421 -68.915 -34.345 -16.394 1.657 34.738 1.002
res[243] -51.824 26.290 -104.250 -69.666 -51.904 -34.191 -0.773 1.002
res[244] -92.310 26.200 -144.512 -109.770 -92.356 -74.742 -41.007 1.002
res[245] 53.225 26.151 1.165 35.773 53.155 70.545 104.484 1.002
res[246] 35.579 26.143 -16.717 18.099 35.633 52.862 86.869 1.001
res[247] -33.204 26.177 -85.575 -50.833 -33.098 -15.939 18.146 1.001
res[248] 35.397 26.252 -16.792 17.809 35.174 52.691 87.176 1.001
res[249] 83.314 26.368 30.491 65.761 83.032 100.631 135.542 1.001
res[250] 42.630 26.524 -9.672 24.976 42.309 59.916 95.055 1.001
res[251] -206.923 27.800 -260.529 -225.880 -206.782 -187.968 -153.986 1.001
res[252] -157.656 27.629 -211.249 -176.383 -157.567 -138.906 -104.887 1.001
res[253] -51.271 27.496 -104.867 -70.030 -51.271 -32.412 1.659 1.001
res[254] 12.860 27.402 -40.341 -5.856 13.103 31.625 65.496 1.001
res[255] 11.898 27.348 -41.371 -7.218 11.887 30.504 64.701 1.001
res[256] -1.747 27.333 -54.813 -20.847 -1.807 16.587 50.997 1.001
res[257] 46.786 27.357 -6.081 27.648 46.704 65.069 100.383 1.001
res[258] 84.114 27.422 31.253 65.110 83.938 102.405 137.813 1.001
res[259] 141.780 27.525 88.996 122.717 141.448 159.933 195.838 1.001
res[260] 140.825 27.667 88.214 121.349 140.766 158.831 195.301 1.001
res[261] -45.758 27.262 -98.677 -63.456 -45.803 -28.120 8.017 1.002
res[262] -73.536 27.103 -126.119 -91.086 -73.677 -55.880 -19.998 1.001
res[263] -66.558 26.984 -118.944 -84.155 -66.732 -49.089 -12.830 1.001
res[264] -3.221 26.904 -55.491 -20.926 -3.268 14.217 50.110 1.001
res[265] 64.093 26.864 12.275 46.220 64.035 81.487 117.920 1.001
res[266] -24.292 26.865 -75.837 -42.281 -24.457 -6.832 29.548 1.001
res[267] 11.470 26.906 -40.398 -6.459 11.267 29.011 65.223 1.001
res[268] 69.347 26.987 17.413 51.396 68.896 87.025 123.112 1.001
res[269] 16.854 27.108 -35.179 -1.244 16.533 34.478 70.967 1.001
res[270] 75.619 27.268 23.067 57.629 75.329 93.227 129.655 1.001
res[271] -225.643 27.480 -278.886 -243.823 -225.694 -207.386 -171.764 1.003
res[272] -140.428 27.320 -193.206 -158.567 -140.609 -122.309 -86.874 1.003
res[273] -92.158 27.198 -145.009 -110.346 -92.252 -74.095 -38.573 1.003
res[274] -37.826 27.116 -90.730 -55.873 -38.139 -19.735 15.494 1.002
res[275] -22.591 27.074 -75.243 -40.456 -22.982 -4.368 30.621 1.002
res[276] 30.930 27.072 -22.094 13.172 30.419 49.127 84.548 1.002
res[277] 103.777 27.109 50.599 85.820 102.988 121.948 157.742 1.002
res[278] 195.528 27.187 142.165 177.513 194.832 213.701 249.967 1.002
res[279] 173.383 27.304 119.414 155.128 172.627 191.796 228.591 1.001
res[280] 48.822 27.460 -5.443 30.590 47.952 67.271 104.943 1.001
res[281] -100.761 27.924 -155.664 -119.211 -100.098 -81.104 -47.734 1.001
res[282] -73.020 27.777 -127.369 -91.266 -72.520 -53.694 -20.563 1.001
res[283] -64.686 27.669 -119.132 -82.823 -64.075 -45.417 -12.494 1.001
res[284] -17.650 27.599 -72.206 -35.666 -17.169 1.377 35.020 1.001
res[285] 46.285 27.569 -7.652 28.252 46.815 65.328 99.260 1.001
res[286] 25.187 27.577 -28.572 7.101 25.553 44.083 78.569 1.001
res[287] 23.689 27.625 -29.512 5.427 23.865 42.895 77.192 1.001
res[288] 61.274 27.713 8.220 42.691 61.404 80.495 114.966 1.001
res[289] 48.126 27.838 -5.127 29.210 48.155 67.369 102.003 1.001
res[290] 73.868 28.002 20.444 54.993 73.670 93.109 128.079 1.001
res[291] -62.043 27.792 -115.822 -80.494 -62.779 -43.673 -4.435 1.001
res[292] -78.060 27.657 -131.681 -96.527 -78.957 -60.027 -21.083 1.001
res[293] -97.080 27.560 -150.130 -115.697 -97.882 -79.080 -40.450 1.001
res[294] -84.403 27.502 -137.305 -103.193 -85.127 -66.419 -27.873 1.001
res[295] -62.058 27.484 -115.409 -80.974 -62.634 -43.885 -5.395 1.001
res[296] 13.785 27.505 -39.891 -5.375 13.338 32.209 69.885 1.001
res[297] 108.636 27.565 55.243 89.343 108.404 127.130 164.689 1.001
res[298] 103.229 27.665 49.562 83.789 102.942 122.033 159.137 1.001
res[299] 89.617 27.803 35.620 70.171 89.485 108.312 146.507 1.001
res[300] 80.672 27.979 26.414 60.959 80.808 99.562 137.744 1.001
res[301] -141.883 28.305 -196.509 -160.420 -141.920 -123.442 -84.721 1.001
res[302] -106.210 28.157 -160.120 -124.453 -106.309 -87.823 -49.394 1.001
res[303] -37.352 28.047 -91.475 -55.335 -37.285 -19.229 19.895 1.001
res[304] -18.327 27.975 -72.662 -36.286 -18.237 -0.397 38.713 1.001
res[305] -86.778 27.942 -140.890 -105.114 -86.791 -68.788 -29.209 1.001
res[306] -37.999 27.947 -91.849 -56.327 -37.867 -20.131 19.461 1.001
res[307] 69.141 27.991 14.641 50.665 69.178 86.859 126.516 1.001
res[308] 159.261 28.074 104.599 140.704 159.387 177.180 216.359 1.001
res[309] 136.516 28.195 80.873 118.244 136.554 154.819 193.892 1.001
res[310] 84.565 28.354 28.496 66.131 84.693 102.951 142.719 1.002
res[311] 8.480 27.336 -47.030 -9.792 8.978 27.073 59.498 1.003
res[312] 11.977 27.128 -43.062 -5.921 12.427 30.119 62.594 1.003
res[313] 22.210 26.959 -32.858 4.243 22.751 40.219 72.580 1.003
res[314] 60.484 26.829 5.199 42.716 60.942 78.598 110.330 1.002
res[315] -6.440 26.739 -61.507 -24.246 -6.091 11.508 43.556 1.002
res[316] -11.502 26.689 -66.443 -29.364 -11.033 6.418 38.397 1.002
res[317] -51.977 26.680 -107.165 -69.981 -51.390 -33.782 -1.318 1.002
res[318] -37.802 26.711 -93.392 -55.747 -37.309 -19.574 12.624 1.002
res[319] 18.322 26.783 -37.480 0.309 19.012 36.680 68.620 1.001
res[320] -6.770 26.895 -62.754 -24.603 -5.931 11.437 44.809 1.001
res[321] -169.878 27.641 -225.412 -188.557 -170.087 -150.812 -115.846 1.003
res[322] -115.245 27.475 -170.155 -133.481 -115.610 -96.509 -61.338 1.002
res[323] -127.030 27.348 -181.991 -145.028 -127.405 -108.460 -73.235 1.002
res[324] -75.745 27.260 -130.493 -94.150 -76.056 -57.347 -21.877 1.002
res[325] -4.442 27.211 -59.066 -22.893 -4.731 14.091 49.373 1.002
res[326] 72.438 27.202 17.923 54.115 72.083 90.962 125.624 1.002
res[327] 74.431 27.233 20.320 56.096 74.054 93.130 128.264 1.001
res[328] 86.173 27.303 32.254 68.056 86.103 104.893 140.473 1.001
res[329] 100.100 27.413 46.110 82.027 100.161 118.754 154.311 1.001
res[330] 191.836 27.562 137.087 173.612 191.900 210.527 246.650 1.001
res[331] -3.568 27.677 -58.111 -22.218 -3.240 14.872 51.330 1.001
res[332] 35.490 27.505 -18.504 16.700 35.467 53.896 89.971 1.001
res[333] 14.836 27.372 -38.705 -3.945 14.883 33.326 69.479 1.001
res[334] 35.529 27.278 -17.795 16.742 35.624 53.845 89.880 1.001
res[335] 57.772 27.224 4.745 39.406 57.712 76.032 112.258 1.001
res[336] 7.505 27.209 -45.201 -11.277 7.241 25.550 61.787 1.001
res[337] -62.853 27.234 -115.231 -81.656 -63.102 -44.830 -8.470 1.001
res[338] 3.554 27.299 -48.771 -15.196 3.261 21.590 57.887 1.001
res[339] -47.691 27.403 -100.181 -66.462 -48.175 -29.624 6.870 1.001
res[340] -7.951 27.546 -60.486 -26.990 -8.417 10.133 47.240 1.001
res[341] -167.838 27.534 -221.260 -186.767 -167.997 -149.518 -113.530 1.005
res[342] -109.245 27.409 -162.241 -128.030 -109.426 -91.138 -55.319 1.005
res[343] -76.905 27.323 -129.335 -95.553 -76.780 -58.727 -23.086 1.004
res[344] -92.961 27.276 -144.845 -111.585 -92.688 -74.742 -39.601 1.004
res[345] -15.658 27.269 -67.414 -34.298 -15.410 2.716 37.316 1.004
res[346] 87.984 27.302 36.319 69.290 88.171 106.278 140.902 1.003
res[347] 132.212 27.374 80.204 113.503 132.167 150.380 185.832 1.003
res[348] 30.540 27.486 -21.770 11.869 30.461 48.883 84.590 1.003
res[349] 120.550 27.636 67.565 101.960 120.450 138.866 174.815 1.002
res[350] 123.963 27.825 70.604 105.055 123.691 142.633 178.437 1.002
sigma 86.053 4.095 78.239 83.300 85.994 88.737 94.268 1.013
sigma.B 317.817 38.958 252.469 291.832 313.873 339.888 405.125 1.002
deviance 4111.820 21.476 4069.687 4097.266 4111.765 4126.251 4152.352 1.008
n.eff
beta[1] 1400
beta[2] 230
gamma[1] 1000
gamma[2] 3000
gamma[3] 1300
gamma[4] 2800
gamma[5] 3000
gamma[6] 3000
gamma[7] 1800
gamma[8] 3000
gamma[9] 1800
gamma[10] 2900
gamma[11] 3000
gamma[12] 1800
gamma[13] 1900
gamma[14] 3000
gamma[15] 3000
gamma[16] 1300
gamma[17] 1100
gamma[18] 3000
gamma[19] 3000
gamma[20] 3000
gamma[21] 3000
gamma[22] 3000
gamma[23] 1800
gamma[24] 3000
gamma[25] 810
gamma[26] 3000
gamma[27] 1500
gamma[28] 570
gamma[29] 3000
gamma[30] 3000
gamma[31] 3000
gamma[32] 660
gamma[33] 730
gamma[34] 3000
gamma[35] 340
res[1] 1100
res[2] 1200
res[3] 1400
res[4] 1700
res[5] 2100
res[6] 2700
res[7] 3000
res[8] 3000
res[9] 3000
res[10] 3000
res[11] 3000
res[12] 3000
res[13] 3000
res[14] 3000
res[15] 3000
res[16] 3000
res[17] 3000
res[18] 3000
res[19] 3000
res[20] 3000
res[21] 1200
res[22] 1400
res[23] 1700
res[24] 2000
res[25] 2500
res[26] 3000
res[27] 3000
res[28] 3000
res[29] 3000
res[30] 3000
res[31] 3000
res[32] 3000
res[33] 3000
res[34] 3000
res[35] 3000
res[36] 3000
res[37] 3000
res[38] 3000
res[39] 3000
res[40] 3000
res[41] 3000
res[42] 3000
res[43] 3000
res[44] 3000
res[45] 3000
res[46] 3000
res[47] 3000
res[48] 3000
res[49] 3000
res[50] 3000
res[51] 3000
res[52] 2800
res[53] 2200
res[54] 1700
res[55] 1400
res[56] 1200
res[57] 1000
res[58] 710
res[59] 630
res[60] 550
res[61] 2000
res[62] 2400
res[63] 3000
res[64] 3000
res[65] 3000
res[66] 3000
res[67] 3000
res[68] 3000
res[69] 3000
res[70] 3000
res[71] 3000
res[72] 3000
res[73] 3000
res[74] 3000
res[75] 3000
res[76] 3000
res[77] 3000
res[78] 3000
res[79] 3000
res[80] 3000
res[81] 2100
res[82] 2600
res[83] 3000
res[84] 3000
res[85] 3000
res[86] 3000
res[87] 3000
res[88] 3000
res[89] 3000
res[90] 3000
res[91] 3000
res[92] 3000
res[93] 3000
res[94] 3000
res[95] 3000
res[96] 3000
res[97] 3000
res[98] 3000
res[99] 3000
res[100] 3000
res[101] 3000
res[102] 3000
res[103] 3000
res[104] 3000
res[105] 3000
res[106] 3000
res[107] 3000
res[108] 3000
res[109] 3000
res[110] 3000
res[111] 1700
res[112] 1400
res[113] 1100
res[114] 980
res[115] 840
res[116] 740
res[117] 650
res[118] 580
res[119] 600
res[120] 480
res[121] 1600
res[122] 2000
res[123] 2400
res[124] 3000
res[125] 3000
res[126] 3000
res[127] 3000
res[128] 3000
res[129] 3000
res[130] 3000
res[131] 3000
res[132] 3000
res[133] 3000
res[134] 3000
res[135] 3000
res[136] 3000
res[137] 3000
res[138] 3000
res[139] 2700
res[140] 3000
res[141] 3000
res[142] 3000
res[143] 3000
res[144] 3000
res[145] 3000
res[146] 3000
res[147] 3000
res[148] 3000
res[149] 3000
res[150] 3000
res[151] 1600
res[152] 1900
res[153] 2300
res[154] 3000
res[155] 3000
res[156] 3000
res[157] 3000
res[158] 3000
res[159] 3000
res[160] 3000
res[161] 1000
res[162] 1200
res[163] 1400
res[164] 1700
res[165] 2100
res[166] 2600
res[167] 3000
res[168] 3000
res[169] 3000
res[170] 3000
res[171] 3000
res[172] 3000
res[173] 3000
res[174] 3000
res[175] 3000
res[176] 3000
res[177] 2700
res[178] 2200
res[179] 2000
res[180] 1500
res[181] 3000
res[182] 3000
res[183] 3000
res[184] 3000
res[185] 3000
res[186] 3000
res[187] 3000
res[188] 3000
res[189] 3000
res[190] 3000
res[191] 3000
res[192] 3000
res[193] 3000
res[194] 3000
res[195] 3000
res[196] 2500
res[197] 2000
res[198] 1700
res[199] 1400
res[200] 1200
res[201] 3000
res[202] 3000
res[203] 2700
res[204] 2100
res[205] 1700
res[206] 1400
res[207] 1200
res[208] 1000
res[209] 890
res[210] 1100
res[211] 3000
res[212] 3000
res[213] 3000
res[214] 3000
res[215] 3000
res[216] 3000
res[217] 3000
res[218] 3000
res[219] 3000
res[220] 3000
res[221] 1800
res[222] 2200
res[223] 2800
res[224] 3000
res[225] 3000
res[226] 3000
res[227] 3000
res[228] 3000
res[229] 3000
res[230] 3000
res[231] 3000
res[232] 3000
res[233] 3000
res[234] 3000
res[235] 3000
res[236] 3000
res[237] 3000
res[238] 3000
res[239] 3000
res[240] 3000
res[241] 900
res[242] 1000
res[243] 1200
res[244] 1400
res[245] 1800
res[246] 2200
res[247] 2800
res[248] 3000
res[249] 3000
res[250] 3000
res[251] 3000
res[252] 3000
res[253] 3000
res[254] 3000
res[255] 3000
res[256] 3000
res[257] 3000
res[258] 3000
res[259] 2600
res[260] 2100
res[261] 1600
res[262] 1900
res[263] 2400
res[264] 3000
res[265] 3000
res[266] 3000
res[267] 3000
res[268] 3000
res[269] 3000
res[270] 3000
res[271] 590
res[272] 650
res[273] 730
res[274] 830
res[275] 960
res[276] 1100
res[277] 1200
res[278] 1500
res[279] 1800
res[280] 2500
res[281] 3000
res[282] 3000
res[283] 3000
res[284] 3000
res[285] 3000
res[286] 3000
res[287] 3000
res[288] 3000
res[289] 3000
res[290] 2800
res[291] 3000
res[292] 3000
res[293] 3000
res[294] 3000
res[295] 3000
res[296] 3000
res[297] 3000
res[298] 3000
res[299] 3000
res[300] 3000
res[301] 3000
res[302] 3000
res[303] 3000
res[304] 3000
res[305] 3000
res[306] 3000
res[307] 3000
res[308] 2700
res[309] 2300
res[310] 1700
res[311] 610
res[312] 670
res[313] 760
res[314] 860
res[315] 990
res[316] 1200
res[317] 1400
res[318] 1700
res[319] 2100
res[320] 2600
res[321] 770
res[322] 870
res[323] 1000
res[324] 1200
res[325] 1400
res[326] 1600
res[327] 2000
res[328] 2600
res[329] 2700
res[330] 3000
res[331] 3000
res[332] 3000
res[333] 3000
res[334] 3000
res[335] 3000
res[336] 3000
res[337] 3000
res[338] 3000
res[339] 3000
res[340] 3000
res[341] 350
res[342] 380
res[343] 420
res[344] 460
res[345] 510
res[346] 570
res[347] 810
res[348] 740
res[349] 1200
res[350] 1500
sigma 130
sigma.B 3000
deviance 200
For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
DIC info (using the rule, pD = var(deviance)/2)
pD = 229.5 and DIC = 4341.4
DIC is an estimate of expected predictive error (lower deviance is better).Given that Time cannot be randomized, there is likely to be a temporal dependency structure to the data. The above analyses assume no temporal dependency - actually, they assume that the variance-covariance matrix demonstrates a structure known as sphericity. Lets specifically model in a first order autoregressive correlation structure in an attempt to accommodate the expected temporal autocorrelation.
> modelString3="
+ model {
+ #Likelihood
+ y[1]~dnorm(mu[1],tau)
+ mu[1] <- eta1[1]
+ eta1[1] ~ dnorm(eta[1], taueps)
+ eta[1] <- inprod(beta[],X[1,]) + gamma[Block[1]]
+ res[1] <- y[1]-mu[1]
+ for (i in 2:n) {
+ y[i]~dnorm(mu[i],tau)
+ mu[i] <- eta1[i]
+ eta1[i] ~ dnorm(temp[i], taueps)
+ temp[i] <- eta[i] + -rho*(mu[i-1]-y[i-1])
+ eta[i] <- inprod(beta[],X[i,]) + gamma[Block[i]]
+ res[i] <- y[i]-mu[i]
+ }
+ beta ~ dmnorm(a0,A0)
+ for (i in 1:nBlock) {
+ gamma[i] ~ dnorm(0, tau.B) #prior
+ }
+ rho ~ dunif(-1,1)
+ tau <- pow(sigma,-2)
+ sigma <- z/sqrt(chSq)
+ z ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq ~ dgamma(0.5, 0.5)
+ taueps <- pow(sigma.eps,-2)
+ sigma.eps <- z/sqrt(chSq.eps)
+ z.eps ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq.eps ~ dgamma(0.5, 0.5)
+ tau.B <- pow(sigma.B,-2)
+ sigma.B <- z/sqrt(chSq.B)
+ z.B ~ dnorm(0, 0.0016)I(0,) #1/25^2 = 0.0016
+ chSq.B ~ dgamma(0.5, 0.5)
+ sd.y <- sd(res)
+ sd.block <- sd(gamma)
+ }
+ "
>
> ## write the model to a text file
> writeLines(modelString3, con = "matrixModel3.txt")
>
> Xmat <- model.matrix(~Time,data.rm)
> data.rm.list <- with(data.rm,
+ list(y=y,
+ Block=as.numeric(Block),
+ X=Xmat,
+ n=nrow(data.rm),
+ nBlock=length(levels(Block)),
+ a0=rep(0,ncol(Xmat)), A0=diag(ncol(Xmat))
+ )
+ )
>
> params <- c("beta",'gamma',"sigma","sigma.B","res",'sigma.eps','rho','sd.y','sd.block')
> adaptSteps = 1000
> burnInSteps = 3000
> nChains = 2
> numSavedSteps = 3000
> thinSteps = 1
> nIter = burnInSteps+ceiling((numSavedSteps * thinSteps)/nChains)
>
> data.rm.r2jags.mt <- jags(data = data.rm.list, inits = NULL, parameters.to.save = params,
+ model.file = "matrixModel3.txt", n.chains = nChains, n.iter = nIter,
+ n.burnin = burnInSteps, n.thin = thinSteps)
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 350
Unobserved stochastic nodes: 393
Total graph size: 3931
Initializing model
>
> data.rm.mt.mcmc <- data.rm.r2jags.mt$BUGSoutput$sims.matrix
> summary(as.mcmc(data.rm.mt.mcmc[,grep('beta|sigma|rho',colnames(data.rm.mt.mcmc))]))
Iterations = 1:3000
Thinning interval = 1
Number of chains = 1
Sample size per chain = 3000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
beta[1] 0.1093 1.0090 0.018422 0.018422
beta[2] 9.1917 1.0421 0.019026 0.019026
rho 0.6991 0.1635 0.002985 0.002985
sigma 63.1901 7.6813 0.140241 0.140241
sigma.B 314.5779 38.4731 0.702419 0.702419
sigma.eps 32.8263 9.4551 0.172625 0.172625
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
beta[1] -1.8402 -0.5698 0.09792 0.7920 2.0576
beta[2] 7.2315 8.4966 9.19938 9.8961 11.2232
rho 0.4549 0.5508 0.68313 0.8453 0.9746
sigma 49.8811 56.9814 62.70134 69.5262 77.4328
sigma.B 251.2601 286.7395 310.40901 338.2187 398.3167
sigma.eps 14.8598 25.5907 35.65555 40.2488 46.3558
>
> #head(data.rm.r2jags.mt$BUGSoutput$sims.list[[c('beta','rho','sigma')]])
> #print(data.rm.r2jags.mt)
> data.rm.mcmc.list.mt <- as.mcmc(data.rm.r2jags.mt)
> Data.Rm.mcmc.list.mt <- data.rm.mcmc.list.mt
>
> # R2 calculations
> Xmat <- model.matrix(~Time, data.rm)
> coefs <- data.rm.r2jags.mt$BUGSoutput$sims.list[['beta']]
> fitted <- coefs %*% t(Xmat)
> X.var <- aaply(fitted,1,function(x){var(x)})
> X.var[1:10]
1 2 3 4 5 6 7 8
814.3418 591.0181 634.1438 685.5362 900.1883 740.2397 864.5962 435.7952
9 10
672.4743 584.2064
>
> Z.var <- data.rm.r2jags.mt$BUGSoutput$sims.list[['sd.block']]^2
> R.var <- data.rm.r2jags.mt$BUGSoutput$sims.list[['sd.y']]^2
> R2.marginal <- (X.var)/(X.var+Z.var+R.var)
> R2.marginal <- data.frame(Mean=mean(R2.marginal), Median=median(R2.marginal), HPDinterval(as.mcmc(R2.marginal)))
> R2.conditional <- (X.var+Z.var)/(X.var+Z.var+R.var)
> R2.conditional <- data.frame(Mean=mean(R2.conditional),
+ Median=median(R2.conditional), HPDinterval(as.mcmc(R2.conditional)))
> R2.block <- (Z.var)/(X.var+Z.var+R.var)
> R2.block <- data.frame(Mean=mean(R2.block), Median=median(R2.block), HPDinterval(as.mcmc(R2.block)))
> R2.res<-(R.var)/(X.var+Z.var+R.var)
> R2.res <- data.frame(Mean=mean(R2.res), Median=median(R2.res), HPDinterval(as.mcmc(R2.res)))
>
> (r2 <- rbind(R2.block=R2.block, R2.marginal=R2.marginal, R2.res=R2.res, R2.conditional=R2.conditional))
Mean Median lower upper
R2.block 0.52595295 0.52197768 0.40289527 0.6376026
R2.marginal 0.07190426 0.06983026 0.03887103 0.1087763
R2.res 0.40214279 0.40351594 0.28261806 0.5200679
R2.conditional 0.59785721 0.59648406 0.47993214 0.7173819It would appear that the incorporation of a first order autocorrelation structure is indeed appropriate. The degree of correlation between successive points is \(0.733\). Let’s have a look at a summary figure.
> coefs <- data.rm.r2jags.mt$BUGSoutput$sims.list[['beta']]
> newdata <- with(data.rm, data.frame(Time=seq(min(Time, na.rm=TRUE), max(Time, na.rm=TRUE), len=100)))
> Xmat <- model.matrix(~Time, newdata)
> pred <- (coefs %*% t(Xmat))
> pred <- adply(pred, 2, function(x) {
+ data.frame(Mean=mean(x), Median=median(x, na.rm=TRUE), t(quantile(x,na.rm=TRUE)),
+ HPDinterval(as.mcmc(x)),HPDinterval(as.mcmc(x),p=0.5))
+ })
> newdata <- cbind(newdata, pred)
> #Also calculate the partial observations
> Xmat <- model.matrix(~Time, data.rm)
> pred <- colMeans(as.vector(coefs %*% t(Xmat))+data.rm.r2jags.mt$BUGSoutput$sims.list[['res']])
> part.obs <- cbind(data.rm,Median=pred)
>
> ggplot(newdata, aes(y=Median, x=Time)) +
+ geom_point(data=part.obs, aes(y=Median))+
+ geom_ribbon(aes(ymin=lower, ymax=upper), fill='blue',alpha=0.2) +
+ geom_line()+
+ scale_x_continuous('Time') +
+ scale_y_continuous('Y') +
+ theme_classic() +
+ theme(axis.title.y = element_text(vjust=2, size=rel(1.2)),
+ axis.title.x = element_text(vjust=-2, size=rel(1.2)),
+ plot.margin=unit(c(0.5,0.5,2,2), 'lines'))